Jutro zaliczenie roku na dwójkę. Błagam o pomoc. Paweł: Dana jest funkcja kwadratowa f(x) = − (x+3)²+2 A) Podaj postać ogólna funkcji oraz współczynniki a,b,c tej funkcji. B) Wyznacz współrzędne wierzchołka paraboli. C) Oblicz miejsca zerowe tej funkcji i zapisz wzór w postaci iloczynowej (jeśli istnieje). D) Zapisz równanie osi symetrii tej funkcji. E) Podaj zbiór wartości funkcji.

zef: Co umiesz ?

Janek191: a) f(x) = − ( x + 3)² + 2 = − ( x² + 6 x + 9) + 2 = − x² − 6 x − 9 + 2 = − x² − 6 x − 7 a = − 1 b = − 6 c = − 7

Janek191: b) f(x) = a*(x − p)² + q W = ( p, q ) f(x) = − ( x + 3)² + 2 więc W = ( − 3, 2) =========== lub f(x) = − x² − 6 x − 7

	− b		6
p =		=		= − 3
	2a		−2

q = f(p) = f(−3) = − ( −3)² − 6*(−3) − 7 = − 9 + 18 − 7 = 2 W = ( − 3, 2) ==========

Janek191: c) f(x) = − x² − 6 x − 7 Δ = b² − 4ac = (−6)² − 4*(−1)*(−7) = 36 − 28 = 8 = 4*2 √Δ = 2√2

	− b − √Δ		6 − 2√2
x1 =		=		= − 3 + √2
	2a		− 2

	− b + √Δ		6 + 2√2
x2 =		=		= − 3 − √2
	2a		−2

f(x) = a*(x − x₁)*(x − x₂) a = − 1 więc f(x) = − [ x − ( − 3 + √2)]*[ x − ( − 3 − √2)] = −( x + 3 − √2)*(x + 3 + √2)

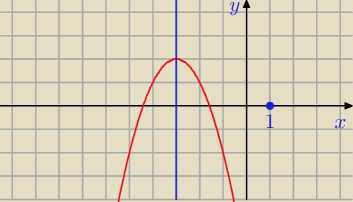
Janek191: d) x = p f(x) = − x² − 6 x − 7

	− b		6
p =		=		= − 3
	2a		−2

x = − 3 =====

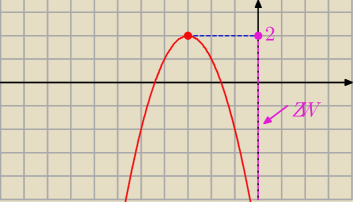
Janek191: a < 0 to ZW = ( −∞; q > czyli ZW = ( − ∞, 2> ===========

Paweł : Janek, jesteś wielki. Dzięki!

Janek191: f(x) = a x² + b x + c − postać ogólna f(x) = a*(x − p)² + q − postać kanoniczna f(x) = a*(x − x₁)*(x − x₂) − postać iloczynowa, gdy Δ > 0 Δ = b² − 4 a*c q można policzyć też z wzoru

	− Δ
q =
	4 a