macierze Ewelina: Wyznacznik macierzy 1 0 −1 −2 1 −1 0 1 −1 −1−0+2−0+1+1=3 Det A =3 Dobrze licze?

Ewelina: ?

Ewelina: .

6latek : Ewelina Nie przyjmnij tego jako wymądrzanie się . Ty jesteś studentka wiec powinnas znac jakies programy do liczenia wyznacznikow chociażby wolfram czy jakies kalkulatory

Ewelina: Okej

Jack: oczywiscie zle. wyznacznik 3−ciego stopnia liczysz uzywajac reguly sarrusa.

Jack: przepisuje 2 pierwsze wiersze [ 1 0 −1] [−2 1 −1] [ 0 1 −1] 1 0 −1 −2 1 −1 no i licze. det A = − 1 + 2 + 0 + 0 + 1 − 0 = 2

Mariusz: 1*1*(−1)+(−2)*1*(−1)+0*0*(−1)−((−1)*1*0+(−1)*1*1+(−1)*0*(−2)) −1+2+0−(−1)=−1+1+2=2

Benny: Można też rozwinięcie Laplace'a Do drugiego wiersza dodaje 2 pierwsze i dostaje: 1 0 −1 0 1 −3 0 1 −1 1*(−1)¹⁺¹*det 1 −3 1 −1 =−1+3=2

Mariusz: Można bez dopisywania wierszy bądź kolumn w pamięci policzyć

Jack: @Benny przy wyznaczniku 3−ciego stopnia to wg mnie nie jest potrzebne rozwiniecie Laplace'a, ale jak najbardziej mozna @Mariusz oczywiscie ze mozna, jednak ja jako poczatkujacy, zawsze sobie dopisuje zeby mi bylo latwiej policzyc.

Mariusz: Rozwinięcie Laplace jest bardziej ogóle niż reguła Sarrusa ale podobnie jak metoda permutacyjna ma złożoność silni

Mariusz: Wypisujemy permutacje zbioru {1,2,...,n} Obliczamy iloczyn elementów a_{i p(i)} oraz zliczamy przestawienia elementów w permutacji {1,2,..,n} konieczne do uzyskania permutacji p(i) Jeżeli liczba przestawień elementów jest parzysta to sumujemy ją ze znakiem + Jeżeli liczba przestawień elementów jest nieparzysta to sumujemy ją ze znakiem −

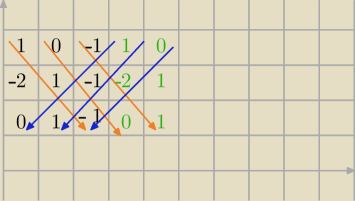
Mila: 1 0 −1 −2 1 −1 0 1 −1 −−−−−−−−−−−−−−−−−−−− W=1*1*(−1)+0*(−1)*0+(−1)*(−2)*1−[0*(−2)*(−1)+1*(−1)*1+(−1)*1*0]= −1+0+2+1=2

Mariusz: Dla większych stopni to nie zadziała Metoda sumowania iloczynów po wszystkich permutacjach elementów zbioru {1,2,3,...,n} wtedy zadziała Drugie indeksy każdego iloczynu tworzą permutację zbioru {1,2,3,...,n}