znowu ja, funkcja kwadratowa, nie zdam, prosze o pomoc crazymofo: Wyznacz współczynniki b i c funkcji kwadratowej f(x)= x²+bc+c jesli zbioerm wartości f jest zbiór wartości <−1,∞) a jej wykres przecina oś OY w punkcie (0,1)

6latek : No musisz troche pomyslec Z tresci zadania wiemy ze a=1 Zbior wartosci funkcji <−1,∞) czyli wspolrzedna y_owa wierzchokla paraboli wynosi (−1) czyli inaczej zapiszmy to q=−1 Jej wykres przecina os OY w punkcie (0,1) Ze wzoru y=ax²+bx+c to wlasnie wspolczynnik c informuje nas o tym w jakim miejscu wykres przecina Os OY czyli nasz c=1 bo wykres przecina os OY w 1 no to masz juz y=x²+bx+1 Teraz sam pomysl nad tym jak wyznaczyc b

6latek : a tam masz x²+bc+c ? czy ma byc x²+bx+c?

crazymofo: x² +bx+c przepraszam, pomyliłam się

kus: jak nie wiadomo co robić to ja zawszę deltę obliczam XD

crazymofo: nie wiem czy to wyszłoby w tym przypadku haha

ICSP:

	b
xw = −
	2

f(x_w) = − 1 Zostanie do rozwiazania jedno równanie kwadratowe.

6latek : Zrobione ?

crazymofo: wyszło mi że b to −2 aczkolwiek nie wiem czy dobrze zrobilam

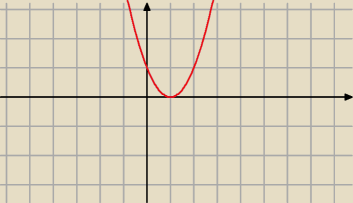
6latek : No to aczkolwiek narysujmy wykres tej funkcji y=x²−2x+1 Niedobrze bo zbior wartosaci tej funkcji to <0,∞) a ma być <−1,∞)

prosta: wtedy wzór funkcji: f(x)=x²−2x+1=(x−1)² −−−−> W=(1,0) niedobrze

crazymofo: to ja nie wiem, chyba nie zdam

6latek : No to pokaz jak liczylas

crazymofo: podstawilam do iloczynowej

prosta: przecież nie znasz x₁ i x₂ ....iloczynowa nie przyda się lepiej wziąć kanoniczną

6latek : Ale tutaj nie masz postaci iloczynowej tylko ogolna Zrob tak jak napisał ICSP

crazymofo: macie racje, to jest dla mnie naprawde czarna magia

6latek : Dobrze . Poprowadzi Cie prosta Dwoje to za dużo

ICSP: f(x) = x² + bx + 1

	−b
xw =
	2

f(x_w) = −1

b2		b2
	−		+ 1 = − 1
4		2

i dalej.

prosta: albo postać kanoniczna: f(x)=(x−p)²−1 i f(0)=1 1=p²−1 p²=2 p=√2 lub p=−√2

	−b
p=xw=		−−−−> b=−2p
	2a

stąd b=−2√2 lub b=2√2

crazymofo: chyba łatwiej podstawić pod kanoniczną

6latek : A rozumiesz to w ogole ?

crazymofo: no własnie nie

6latek : To będzie w takim razie problem duzy Będziesz musiala odwiedzić swojego nauczyciela .

crazymofo: No własnie z nauczycielem mam problem, jutro mam poprawę testu, niestety, jeszcze spróbuję to zrobić, może ogarnę i dziękuje za cierpliwość i pomoc

6latek : Do postu 15:47 Wzor na wspolrzedna x_w wierzchołka paraboli jest taki x_w= U{−b}[2a}

	−b
nasze a=1 tutaj wiec xw=
	2

Wartosc funkcji w x_w=q naszse q=−1 funkcja nasza ma taki wzor f(x_w)=−1 piszsemy x²+bx+1=−1

	−b
(−b}{2})2+b*		+1=−1
	2

b2		b2
	−		+1= −1 (obie strony równania mnożymy przez 4 żeby pozbyć się mianownika
4		2

	b2		−b2
4*		−4*		+4*1=4*(−1)
	4		2

b²−2b²+4=−4 −b²=−4−4 −b²=−8 b²=8 to b=√8= 2√2 lub b=−√8 = −2√2

crazymofo: już jaśniej, bardzo dziękuje