zadanie hh: oblicz pole koła wpisanego w trójkąt prostokątny wiedząc że wysokość tego trójkąta poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki długości 2 i 6 Sprawdzałam kilka razy ale w odpowiedziach są inne wyniki a mianowicie :8pi(2−sqrt(3)) ale nie rozumiem dlaczego przecież skoro promień okręgu wpisanego jest prostopadły do przeciwprostokątnej to musi się pokrywać z wysokością prawda? Czy to może chodzi o jakąś cechę podobieństwa? tak czy inaczej korzystałam z twierdzenia Pitagorasa (r+6)² + (r+2)²=8²

g: Z podobieństwa trójkątów: 2/h = h/6, h = √12 Pole trójkąta = 1/2 * 8 * h = 1/2 * a * b = 1/2 * (8+a+b) * r Pitagoras: a² + b² = 8² Mając a*b i (a²+b²) wyznacz a i b (a może od razu a+b), a następnie r.

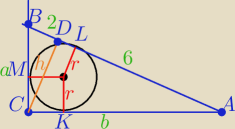
Mila: h=√2*6=√12=2√3

	1
PΔ=		*(2+6)*2√3=8√3
	2

	a+b+c
PΔ=		*r
	2

a²=h²+2² a²=12+4 a=4 b²=h²+6² b²=48 b=4√3

a+b+c		4+4√3+8
	=		=6+2√3
2		2

a+b+c
	*r=8√3
2

(6+2√3)*r=8√3 /*(6−2√3) (36−12)*r=8√3*(6−2√3) 24r=48√3−16*3 r=2√3−2 P_o=π*r²=π*(2√3−2)²=π*(4*3−8√3+4) P_o=π*(16−8√3) P_o=8π*(2−√3) =============

myszka: h²=2*6 =12 c= 2+6=8 a=√2²+12=4 , b= √6²+12= √48=4√3 2r=a+b−c = 4+4√3−8 = 4√3−4 r= 2(√3−1) P=πr² = 4(√3−1)²π= 8π(2−√3) [j²]

Ankaaa: F(x)=(√5•2)X −1

Ankaaa: Miejscem zerowym funkcji liniowej jest