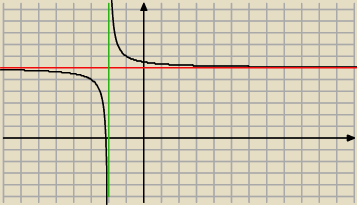
wymierna (wykres + inne 6latek : Może bardzie teorii trochę . mam taka funkcje

	1
f(x)=		+6
	x+2

Z wykresu tej funkcji Przy x dazaącym do nieslkonczonosci wartości tej funkcji dążą do 6 czyli wartości funkcji sa dowolnie bliskie 6 gdy wartości x sa dodtatecznie duże czy mogą roznic się np. od 6 o jedna milionowa(czyli 10⁻⁶ ? Wobec tego czy istnieje takie x₀ ze dla każdego x>x₀ mamy |f(x)−6|<10⁻⁶

	1
|6+		−6|<10−6 czyli
	x+2

	1
|		|<10−6
	x+2

	1		|1|		1
Mogę sobie |		| zapisac tak		=
	x+2		|x+2|		|x+2|

1
	<10−6
|x+2|

teraz mamy ze dla x>−2 |x+2|= x+2

	1		1
Wiec dla x>−2 mamy		<10−6 ⇒U[1}{x+2}<		⇒x+2>106⇒x>106−2
	x+2		106

Pytanie . Dlaczego liczymy tylko dla x>−2 a nie tez dla x<−2? Po uzyskaniu odpowiedzi na to pytanie zadam następne

antoni: we wstępnym opisie mówimy o granicy przy x dążącym do plus nieskończoności, stąd x+2>0

6latek : dzieki

6latek : dalej mozna za x₀ przyjac 10⁶−2 lub dowolna liczbe wieksza od 10⁶−2 np 10⁶ dla kazdego x>10⁶ mamy −10⁻⁶<f(x)−6<10⁻⁶ czyli 5,999999<f(x)<6,000001 Nie bardzo wiem skad to sie wzielo

6latek :

antoni: −10₋6<f(x)−6<10₋6 −10₋6+6<f(x)−6+6<10₋6+6 5,999999<f(x)<6,000001

6latek : Czy tutaj korzystamy z tego ze |m−a|<ε?

antoni: można tak to widzieć...

6latek : dziekuje CI