Objętośc - całka podwójna Mateusz: Oblicz objętość bryły ograniczonej powierzchnią z=2xy oraz powierzchnią wyciętą przez ćwiartkę koła x²+y² ≤25 dla x≤0 y≥0. Bardzo proszę o pomoc, nie mam pojęcia jak się za to zabrać

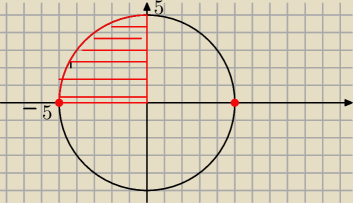
6latek : Cwiartka tego kola to będzie obszar zakreskowany na czerwono wraz z osiami wspolrzednych Natomiast z=2xy (nie wiem jak narysować (brak wiedzy

Jerzy: Przejdż na współrzędne biegunowe: 0 ≤ r ≤ 5

π
	≤ φ ≤ π
2

IVI = ∫∫2rcosφ*rsinφ*rdrdφ

Mateusz: czemu π ≤ φ ≤ π 2 ? bo nie rozumiem tego

Jerzy: bo tak zmienia się kąt po tym obszarze

Mateusz: a moja interpretacja od 0 do π/2 jakby wyglądała?

g: Wzór z = 2xy wyznacza jedną powierzchnię ograniczającą. A gdzie druga? Czy przez domniemanie z = 0 ?

Jerzy: Tak zakładam

Mateusz: a jak policzyć dalej tą całkę ∫∫2rcosφ*rsinφ*rdrdφ ?

Jerzy: = ∫∫r³sin2φdrdφ

Mateusz: −625/4 ?

azeta: liczysz objętość

Mateusz: tak