objetosc bryly
misiak: Romb o boku a i kącie ostrym α obraca się dokoła prostej, przechodzącej przez wierzchołek kąta
ostrego i prostopadłej do jednego z przyległych boków. Znaleźć objętość bryły otrzymanej z
obrotu.
26 maj 19:33
Jerzy:
I gdzie problem... zrób rysunek pzekroju tej bryły
26 maj 19:51
misiak: ok zrobiłem, nadal nie wiem ja to zrobić

26 maj 19:58
Jerzy:
Jakie bryły widzisz ?
26 maj 20:03
misiak: przekroj przedtsawia dwa romby nie wiem co dalej...?
26 maj 20:08
misiak: nie wiem o jakie bryły chodzi
26 maj 20:08
Jerzy:
Mzasz walec, nad nim stożek, a pod spodem z walca wycięto taki sam stożek
26 maj 20:12
misiak: gdy narysuję tę bryłę to we wnętrzu znajduje sie stożek
26 maj 20:14
misiak: faktycznie
26 maj 20:14
misiak: masz racje
26 maj 20:14
Jerzy:
No to po zabawie
26 maj 20:15
misiak: aha

dzieki
26 maj 20:17
misiak: a nie wychodzi przypadkiem tak, że to prosta jest prostopadła do jednego z boków?
i wtedy powstaje bryła, której punktem wspolnym z prostą jest tylko wierzchołek
kąta ostrego rombu?
26 maj 20:29
misiak: i powstanie sciety stożek i w środku wyciety stożek?
26 maj 20:29
Jerzy:
Nie kombinuj...licz objętość walca
26 maj 20:31
misiak: wysokosc;h
sinα=ah
h=a*sinα
wiec objetość walca to πr2*h=π(asinα)2*a=a3π*(sinα)2
tak wychodzi
26 maj 20:37
misiak: wysokosc;h
sinα=ah
h=a*sinα
wiec objetość walca to πr2*h=π(asinα)2*a=a3π*(sinα)2
tak wychodzi
26 maj 20:38
misiak: mi sie jednak wydaje ze to bedzie ten ściety stożek i w środku wyciety i taki przekrój
_______

_______
/ /|\ \
/ / | \ \
/_______

| \______\
26 maj 20:43
misiak:
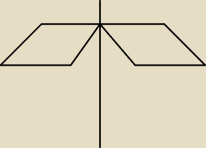
coś nie wyszedł rysunek

26 maj 20:45
misiak: ten na górze jest dobry
26 maj 20:46
misiak:
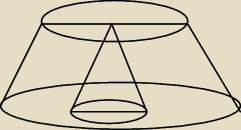
26 maj 20:48
Jerzy:
Kąta ostrego
26 maj 20:50
misiak:
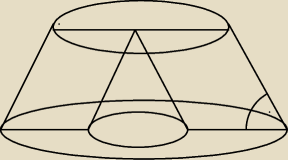
26 maj 20:55
misiak: i wtedy ta prosta przechodzi przez wierzchołek stożka i środek okręgu (tego na dole)
26 maj 20:57
misiak:
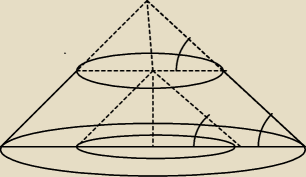
ja to widzę tak: kąt zanaczony na rysunku ma miarę α , tworząca małego stożka na dole ma
długość a
wysokość stożka małego górnego ma długość H, a wysokość małego stożka na dole ma długość h
oraz jego promień ma długość r
sinα=
ha ⇒ h=asinα
cosα=
ra ⇒ r=acosα
tgα=
Ha ⇒ H=atgα
Pf

bjetosc bryly o ktorej mowa w zadaniu P1

bjetosc stożka największego, P2

bjetosc stozka
malego dolnego i P3

bjetosc stożka malego gornego
Pf=P1−P2−P3
P1=
13 π (a+r)
2 * (h+H)=
13 π(a
2+2ar+r
2)(h+H)=
13
π(ha
2+2arh+hr
2+Ha
2+2arH+Hr
2)
P2=
13 π r
2 * h
P3=
13 π a
2 * H
P1−P2−P3=
13 π (ha
2+2arh+hr
2+Ha
2+2arH+Hr
2−r
2 * h − a
2 * H)=
=
13 π (ha
2+2arh+2arH+ Hr
2)=
13 π (a
3 sinα +
2a*acosα*asinα+2a*acosα*atgα+atgα*(acosα)
2)=
=
13 π (a
3 sinα + 2a
3 cosαsinα+2a
3 sinα+a
3 cosαsinα)=
13 π a
3
(sinα+2cosαsiα+2sinα+cosαsinα)=
=
13 π a
3 (3sinα+3cosαsinα)=
13 π a
3 3sinα (1+cosα)
26 maj 22:41
misiak: jeszcze można to uprościć: =π a3 sinα(1+cosα)
27 maj 08:25

 dzieki
dzieki
 _______
/ /|\ \
/ / | \ \
/_______
_______
/ /|\ \
/ / | \ \
/_______ | \______\
| \______\
 coś nie wyszedł rysunek
coś nie wyszedł rysunek 


 ja to widzę tak: kąt zanaczony na rysunku ma miarę α , tworząca małego stożka na dole ma
długość a
wysokość stożka małego górnego ma długość H, a wysokość małego stożka na dole ma długość h
oraz jego promień ma długość r
sinα=ha ⇒ h=asinα
cosα=ra ⇒ r=acosα
tgα=Ha ⇒ H=atgα
Pf
ja to widzę tak: kąt zanaczony na rysunku ma miarę α , tworząca małego stożka na dole ma
długość a
wysokość stożka małego górnego ma długość H, a wysokość małego stożka na dole ma długość h
oraz jego promień ma długość r
sinα=ha ⇒ h=asinα
cosα=ra ⇒ r=acosα
tgα=Ha ⇒ H=atgα
Pf bjetosc bryly o ktorej mowa w zadaniu P1
bjetosc bryly o ktorej mowa w zadaniu P1 bjetosc stożka największego, P2
bjetosc stożka największego, P2 bjetosc stozka
malego dolnego i P3
bjetosc stozka
malego dolnego i P3 bjetosc stożka malego gornego
Pf=P1−P2−P3
P1= 13 π (a+r)2 * (h+H)= 13 π(a2+2ar+r2)(h+H)= 13
π(ha2+2arh+hr2+Ha2+2arH+Hr2)
P2= 13 π r2 * h
P3= 13 π a2 * H
P1−P2−P3= 13 π (ha2+2arh+hr2+Ha2+2arH+Hr2−r2 * h − a2 * H)=
= 13 π (ha2+2arh+2arH+ Hr2)= 13 π (a3 sinα +
2a*acosα*asinα+2a*acosα*atgα+atgα*(acosα)2)=
=13 π (a3 sinα + 2a3 cosαsinα+2a3 sinα+a3 cosαsinα)= 13 π a3
(sinα+2cosαsiα+2sinα+cosαsinα)=
=13 π a3 (3sinα+3cosαsinα)= 13 π a3 3sinα (1+cosα)
bjetosc stożka malego gornego
Pf=P1−P2−P3
P1= 13 π (a+r)2 * (h+H)= 13 π(a2+2ar+r2)(h+H)= 13
π(ha2+2arh+hr2+Ha2+2arH+Hr2)
P2= 13 π r2 * h
P3= 13 π a2 * H
P1−P2−P3= 13 π (ha2+2arh+hr2+Ha2+2arH+Hr2−r2 * h − a2 * H)=
= 13 π (ha2+2arh+2arH+ Hr2)= 13 π (a3 sinα +
2a*acosα*asinα+2a*acosα*atgα+atgα*(acosα)2)=
=13 π (a3 sinα + 2a3 cosαsinα+2a3 sinα+a3 cosαsinα)= 13 π a3
(sinα+2cosαsiα+2sinα+cosαsinα)=
=13 π a3 (3sinα+3cosαsinα)= 13 π a3 3sinα (1+cosα)