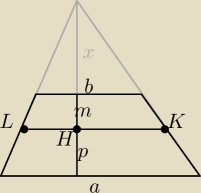
trojkat trojkat: Przez punkt H dzielacy wysokosc trapezu ABCD w stosunku m : p poprowadzono prosta rownolegla do podstawy AB, ktora przecina boki BC i AD odpowiednio w punktach K i L. Wykaz, ze

	ma+pb
KL=		gdzie a=AB i b=CD.
	m+p

Wskazowka: Poprowadz przekatna i zastosuj twierdzenie Talesa.

trojkat: ?

g:

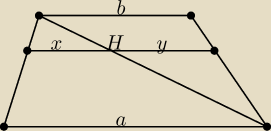
	x		x+m		x+m+p
Tales:		=		=
	b		KL		a

Z jednego równania wyznacz x, wstaw do drugiego i wyznacz KL.

trojkat: A dla przekatnej jakby to wygladalo?

trojkat: ?

prosta:

x		m		y		p
	=		i		=
a		m+p		b		m+p

	ma		pb
x=		i y=
	m+p		m+p

trojkat:

	x		a
A dlaczego nie moge napisac np.		=		? Czy to bedzie zle?
	p		m+p

prosta: przy oznaczeniach jak na rysunkach powyżej nie będzie to dobrze