zad matthew:

	1
Dla każdej liczby rzeczywistej b rownanie y =		x2 − bx +2 opisuje pewną parabolę.
	2

Wyznacz wszystkie wartości parametru b, dla których wierzchołek paraboli leży nad osią OX. Zrobiłem tak:

	1
y =		x2 − bx +2
	2

Δ = (−b)² − 4 * 2 = b² − 4 1) Δ<0 brak m. zer. b² − 4<0 b²<4 b < 2 ⋀ b < −2 Brak rozw. dla b∊(−∞, 2) Może ktoś sprawdzić to zadnie Dziękuję

kamil: chyba masz błąd w końcówce, chociaż nie zastanawiałem sie w ogóle nad sensem rozumowania. będzie od −2 do 2

Eta:

	−Δ
yw=		>0
	4a

−b2+4
	>0 ....... dokończ
2

kamil: ale wydaje mi się, że dobrze. parabola będzie leżała nad osią x, bo jej ramiona dla każdego b są zwrócone do góry, a delta gwarantuje, że nie spotka się z osią x. chociaż o ile dobrze pamiętam, był jeszcze taki inny wzór na punkt w którym znajduje się jej wierzchołek. ale na 99% dobrze

kamil: o to mi chodziło, pozdrawiam Eta

matthew:

−b2 + 4
	>0 / *2
2

−b² + 4>0 −b²> − 4 b²< 4 b<2 ⋁ b< −2 ....... coś chyba robię źle bo powinno być, że b∊(−2, 2), a tutaj tak nie jest..... Wzór kojarzę , ale nie wiedziałem, ze moze być w tym wypadku potrzebny....

matthew: Mam jeszcze jedno krótkie zadanie... A i B są takimi zdarzeniami losowymi zawartymi w Ω, ze A⊂B oraz P(A) = 0,3 i P(B) = 0,4. Oblicz P(A∪B) Zrobiłem tak: P(A∩B) = P(A) * P(B) P(A∩B) = 0,3 * 0,4 = 0,12 P(A∪B) = 0,3 + 0,4 − 0,12 = 0,58 Będę bardzo wdzięczny za sprawdzenie ...

Eta: nierówność kwadratową rozwiazujemy tak b² −4 <0 => ( b+2)(b −2) <= => b€( −2,2)

matthew: Eta, a możesz sprawdzić to zadanie powyżej....? Na pewno nie da się tej funkcji kwadratowej przekształcić, tak jak ja zrobiłem...? Może coś tylko zepsułem ze znakami <, >? Dzięki za odpowiedzi

matthew: Ponawiam...

Eta: przecież Ci podałam b²<4 rozwiązujemy tak: b² −4 <0 => ( b−2)(b+2) <0 => b€( −2,2)

matthew: Wiem, wiem Ale mam jeszcze takie zadanie : A i B są takimi zdarzeniami losowymi zawartymi w Ω, ze A⊂B oraz P(A) = 0,3 i P(B) = 0,4. Oblicz P(A∪B) Jest powyżej

Eta: Nie mogę odczytać tych znaczków bo u mnie wszystkie są kwadracikami ( nie wiem dlaczego

matthew: ok. trudno.... Jeszcze raz dziekuję za resztę

Eta: napisz czy tam jest U czy ∩

matthew: A i B są takimi zdarzeniami losowymi zawartymi w Ω, ze A⊂B oraz P(A) = 0,3 i P(B) = 0,4. Oblicz P(A∪B) W treści zadania jest ∪

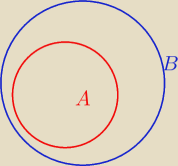
Eta: ponieważ a zawarte w B to AUB= B więc P(AUB) = P(B)= 0,4

Eta: Domyśliłam się i napisałam słownie "zawarte" i "suma" bo u mnie jest kwadracik i znów taki sam kwadracik i nie wiem jaki to był znaczek

matthew: aaa juz wiem, no jasne Dzięki ! A ja mówię Dobranoc...

Eta: Dobranoc, miłych snów nie tylko o prawdopodobieństwie