Dla jakich wartości parametru m równanie ma dwa rózne pierwiastki większe od 1 Darek: Witam, wiem że takie zadanie jest na forum lecz potrzebuję wytłumaczenia, a nie wyniku dla jakich wartości parametru m równanie x² − 2mx + m² − 1 = 0 ma dwa rózne pierwiastki większe od 1 Z założeń na pewno wynika, że Δ > 0 m₁ > 1 m₂ > 1 I mi wyszło coś takiego : {Δ>0 {m₁ + m₂ >2 {m₁ * m₂ >1 I właśnie wiem, że to jest źle i problem leży chyba w ostatnim założeniu. Dodam, że udało mi się rozwiązać te zadanie licząc swoim sposobem, który jest chyba niepoprawny(użyłem tam po prostu delty i wszystko się zgadzało wynikowo) No, ale obliczając poprawnym sposobem dochodzę do sytuacji gdzie: {m należy do R {m > 1 {m należy do (−∞,−√2 ∪ (√2,+∞) A żeby równanie było poprawnie rozwiązane to ostatni warunek zgaduje, że musi być coś takiego (−∞,−2} ∪ (2,+∞) Czy dwa górne warunki są prawidłowe oraz jak poprawnie zapisać ostatni warunek?

Darek: dobra już wyczaiłem bazukę jeżeli ktoś w odległej przyszłości trafił na podobny problem to już piszę wytłumaczenie: ostatnie założenie musi być takie : {(m₁ −1)*(m₂ −1) >0 a to dlatego, że m₁*m₂ nie uwzględnia tego, że m₁ i m₂ muszą być większe od 1 np. w błędnym założeniu m₁ mogłoby wynosić 0,5 ,a m₂ − 3. Warunek( m₁*m₂>1) byłby wtedy spełniony, jednak nie byłby spełniony warunek z polecenia(m₁ i m₂ > 1) −> 0,5*3 >1 a w poprawnym byłoby: 0,5 −1 * 3 −1 = = −0,5 * 2 = = −1 zaś −1 nie jest większe od 1

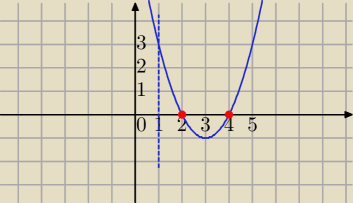
Mila: a=1 ⇔parabola skierowana do góry. Warunki: 1) Δ>0 (dwa różne pierwiastki) 2) f(1)>0

	−b
3) xw=		>1
	2a

Wykres może przebiegać np. tak jak na rysunku. Δ=4m²−4*(m²−1)=4⇔m∊R ⋀ f(1)=m²−2m>0 m*(m−2)>0⇔m<0 lub m>2 ⋀

	2m
xw=		=m
	2

m>0 −−−−−−−−−−−− m>2 ====

andy76sz: Założenia powinny być następujące: 1. Δ>0 2. x₁>1 3. x₂>0 Zatem z 2 i 3 x₁−1>0 i x₂−1>0. Wyróżnienia x₁−1>0 i x₂−1>0 są dodatnie wtedy i tylko wtedy, gdy ich iloczyn jest dodatni i suma dodatnia. Otrzymujemy zatem x₁+x₂−2>0 i x₁x₂−(x₁+x₂)+1>0. Dalej wzory Viete'a.

andy76sz: Oczywiście założenie 3. x₂>1. Dalej bez zmian.