trojkat
trojkat: Wewnatrz trojkata wybieramy dowolny punkt P. Wykaz, ze z odcinkow PAsinA, PBsinB, PCsinC mozna
zbudowac trojkat
.
20 maj 16:26
g:
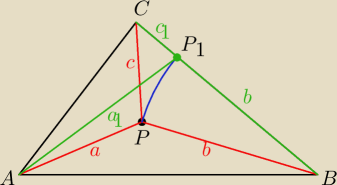
Punkt P rzutuję na jeden z boków, np. na BC, w ten sposób, że |PB| = |P
1B|.
Z twierdzenia sinusów wynikają następujące równania:
c
1 sin C = a
1 sin A
C
b sin B = a
1 sin A
B
gdzie A
C = kąt CAP
1, A
B = kąt BAP
1, A
B+A
C=A
Dodaję te dwa równania
c
1 sin C + b sin B = a
1 (sin A
C + sin A
B) ≥ a
1 sin A
Teraz wracamy z P
1 do P i co widać: a < a
1, c > c
1, zatem musi zachodzić:
c sin C + b sin B ≥ a sin A
Ta nierówność, łącznie z dwoma podobnymi, otrzymanymi z rzutowania P na inne boki
dowodzą możliwości zbudowania trójkąta.
Jest kłopot gdy b > |BC|. Jeszcze pomyślę.
21 maj 11:29
g:
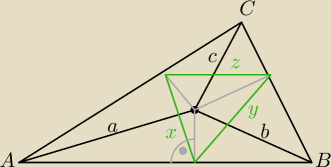
To może inaczej.
x
2 = a
2 sin
2 A
1 + a
2 sin
2 A
2 + 2 a
2 sin A
1 sin A
2 cos A = a
2 sin
2 A
x = a sin A, podobnie y i z.
21 maj 13:01
david:
Dlaczego ? x2= ......= a2*sin2A ( nie rozumiem
21 maj 15:10
g:
sin2A1 + sin2A2 + 2 sinA1 sinA2 (cosA1 cosA2 − sinA1 sinA2) =
sin2A1 + sin2A2 + 2 sinA1 cosA2 sinA2 cos A1 − 2 sin2A1 sin2A2 =
sin2A1 (1 − sin2A2) + sin2A2 (1 − sin2 A1) + 2 sinA1 cosA2 sinA2 cos A1 =
(sin A1 cos A2 + sin A2 cos A1)2 = sin2A
21 maj 17:55
 Punkt P rzutuję na jeden z boków, np. na BC, w ten sposób, że |PB| = |P1B|.
Z twierdzenia sinusów wynikają następujące równania:
c1 sin C = a1 sin AC
b sin B = a1 sin AB
gdzie AC = kąt CAP1, AB = kąt BAP1, AB+AC=A
Dodaję te dwa równania
c1 sin C + b sin B = a1 (sin AC + sin AB) ≥ a1 sin A
Teraz wracamy z P1 do P i co widać: a < a1, c > c1, zatem musi zachodzić:
c sin C + b sin B ≥ a sin A
Ta nierówność, łącznie z dwoma podobnymi, otrzymanymi z rzutowania P na inne boki
dowodzą możliwości zbudowania trójkąta.
Jest kłopot gdy b > |BC|. Jeszcze pomyślę.
Punkt P rzutuję na jeden z boków, np. na BC, w ten sposób, że |PB| = |P1B|.
Z twierdzenia sinusów wynikają następujące równania:
c1 sin C = a1 sin AC
b sin B = a1 sin AB
gdzie AC = kąt CAP1, AB = kąt BAP1, AB+AC=A
Dodaję te dwa równania
c1 sin C + b sin B = a1 (sin AC + sin AB) ≥ a1 sin A
Teraz wracamy z P1 do P i co widać: a < a1, c > c1, zatem musi zachodzić:
c sin C + b sin B ≥ a sin A
Ta nierówność, łącznie z dwoma podobnymi, otrzymanymi z rzutowania P na inne boki
dowodzą możliwości zbudowania trójkąta.
Jest kłopot gdy b > |BC|. Jeszcze pomyślę.
 To może inaczej.
x2 = a2 sin2 A1 + a2 sin2 A2 + 2 a2 sin A1 sin A2 cos A = a2 sin2 A
x = a sin A, podobnie y i z.
To może inaczej.
x2 = a2 sin2 A1 + a2 sin2 A2 + 2 a2 sin A1 sin A2 cos A = a2 sin2 A
x = a sin A, podobnie y i z.