 mam wyznaczyć zbiór A' , B', A∪B, A∩B , A \ B , B \ A gdy:
mam wyznaczyć zbiór A' , B', A∪B, A∩B , A \ B , B \ A gdy:
| 13 | 3 | 4−x | 1 | |||||
A={x∊R; | − | <−4} , B={x∊R; | < | } | ||||
| x−3 | x+1 | x−5 | 1−x |

| 13 | 3 | |||
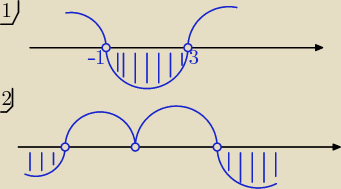
A : | − | < −4 D = R \ {−1, 3} | ||
| x−3 | x+1 |
| 13(x+1) − 3(x−3) + 4(x−3)(x+1) | ||
< 0 | ||
| (x−3)(x+1) |
| 13x+13−3x+9+4(x2+x−3x−3) | ||
< 0 | ||
| (x−3)(x+1) |
| 10x+22+4x2−8x−12 | ||
< 0 | ||
| (x−3)(x+1) |
| 4−x | 1 | |||
B : | < | D = R \ { 1, 5} | ||
| x−5 | 1−x |
| 4−x | 1 | |||
− | < 0 | |||
| x−5 | 1−x |
| (4−x)(1−x) − (x−5) | ||
< 0 | ||
| (x−5)(1−x) |
| 4−4x−x+x2−x+5 | ||
< 0 | ||
| (x−5)(1−x) |
 A' = (−∞, −1> ∪ < 3, ∞)
B' = <1,5>
A ∪ B = (−∞, 3) ∪ (5, ∞)
A ∩ B = ( −1, 1)
A \ B = <1, 3 )
B \ A = ( −∞, −1> ∪ ( 5, ∞)
A' = (−∞, −1> ∪ < 3, ∞)
B' = <1,5>
A ∪ B = (−∞, 3) ∪ (5, ∞)
A ∩ B = ( −1, 1)
A \ B = <1, 3 )
B \ A = ( −∞, −1> ∪ ( 5, ∞)
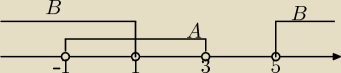
 To i ja wtrącę "trzy grosze"
To i ja wtrącę "trzy grosze"  z takiego zaznaczenia przedziałów, o którym tyle pisze Bogdan
z takiego zaznaczenia przedziałów, o którym tyle pisze Bogdan  wyraźniej widać , które "kółeczka" są w danym przedziale ,
a które są poza przedziałem
A \ B = <1,3)
B \ A= ( −∞−1> U (5,∞)
A' = (−∞,−1> U <3 , ∞)
B'= <1,5>
P.S Warto stosować takie oznaczenia , bardzo pomagają w podaniu poprawnych
odpowiedzi
wyraźniej widać , które "kółeczka" są w danym przedziale ,
a które są poza przedziałem
A \ B = <1,3)
B \ A= ( −∞−1> U (5,∞)
A' = (−∞,−1> U <3 , ∞)
B'= <1,5>
P.S Warto stosować takie oznaczenia , bardzo pomagają w podaniu poprawnych
odpowiedzi szczególnie przy róznicy czy dopełnieniu zbiorów.
Oczywiście Anna podała poprawne rozwiązanie .
szczególnie przy róznicy czy dopełnieniu zbiorów.
Oczywiście Anna podała poprawne rozwiązanie .
 Pora spać
Pora spać 
