F.Logarytmiczna Igor: http://s5.ifotos.pl/img/132312188_sanqrhn.jpg

Igor: Poprosiłbym o rozwiązanie zadania 1 i 3.

Jack: 3. log³₅x − 3log²₅x + 4 = 0 założenie: x>0 Niech log₅x = k k³ − 3k² + 4 = 0 k³ − 2k² − k² + 4 = 0 k²(k−2) − (k² − 4) = 0 k²(k−2) − (k−2)(k+2) = 0 (k−2)(k² − (k+2)) = 0 (k−2)(k² − k − 2) = 0 (k−2)(k−2)(k+1) = 0 (k−2)²(k+1) = 0 k = 2 lub k = − 1 zatem log₅x = 2 lub log₅x = − 1 5² = x lub 5⁻¹ = x

	1
x = 25 lub x =
	5

oba naleza do dziedziny, zatem to jest wynik.

Igor: Czy to na pewno wszystkie założenia?

Jack: a widzisz jakies dodatkowe?

Igor: Właśnie nie pamiętam wgl f,logarytmicznej ale kojarzą mi się 3 założenia obowiązkowe. Jeśli ich nie ma to utrata punktów.

Jack: log_ab = c założenia a > 0, b >0 a≠1 to sa zalozenia. u Ciebie a = 5 , b = x, zatem zalozenia tylko do iksa.

Igor: A dałoby radę poprosić jeszcze o 2 lub 3 zadanie ?

Jack: to bylo zadanie numer 3.

Jack: zadanie 1. zrob na podstawie postu 19:44 sprawdzę.

Igor: x≠3

x−2
3−x

x < 3 i x>2 Z a>0 mam problem ale postaram się sam zrobić.

Igor: No log₇ i liczba logarytmowana czyli ten log₁/7

Igor: log_1/7

Mila: 2) logx+2log(x+1)=logx² x>0 i x+1>0⇔ x>−1 logx+log(x+1)²=logx² log[x*(x+1)²]=logx²⇔ x*(x+1)²=x² x*(x²+2x+1)=x² x*(x²+2x+1)−x²=0 wyłączam x x*[x²+2x+1−x]=0 x=0∉D lub x²+x+1=0 Δ=1−4<0 brak rozwiązania brak rozwiązania.

Mila: (1) w takim razie inaczej niż napisałam. Zaraz.

Igor: Czemu w 2 jak przed nawias dajesz log, + zamienia się w *

Jack: to nie jest wyciaganie log przed nawias. nie mozesz wyciagnac samego log, tak jak masz funkcje sinx + sin(30−x) to nie robisz sin(x+30−x) bo to kompletna bzdura. Korzystasz ze wzoru log_ab + log_ac = log_a(b*c) tak samo jest wzor na odejmowanie

	b
logab − logac = loga(		)
	c

Mila: Jeżeli to taki zapis, to tak:

	x−2
f(x)=log7[log17(		)−1]
	3−x

	x−2		x−2
log17(		)−1>0 i		)⇔
	3−x		3−x

	x−2
[log17(		)>1] i [(x−2)*(3−x)>0]
	3−x

	x−2		1
log17(		)>log1/7(		) i [ x∊(2,3)]
	3−x		7

	1
Podstawa		∊(0,1) zatem funkcja logarytmiczna malejąca⇔
	7

	x−2		1
(		)<		i [ x∊(2,3)]⇔
	3−x		7

x−2		1
	−		<0
3−x		7

7*(x−2)−1*(3−x)
	<0
7*(3−x)

8x−17
	<0 ⇔
7*(3−x)

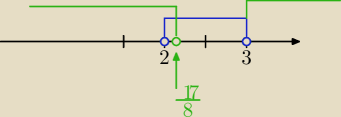
(8x−17)*(3−x)<0 parabola skierowana w dół

	17		1
x=		=2		, x=3
	8		8

	17
[ x<		lub x>3 ] i [ x∊(2,3) ]⇔
	8

	17
D=(2,		)
	8

========== Jeżeli masz pytania to pisz.

Mila: Jak wyjaśnił Jack korzystamy z własności logarytmów, musisz to powtórzyć. Np. log5 +log2=log(5*2)=log(10)=1 log₇(2)+log₇(10)=log₇(2*10)=log₇(20) log x+log(x+5)=log[x*(x+5)] dla x>0 i x+5>0 log5²=2log5 5log7=log(7⁵)

Igor: Zapomniałem po prostu, moja głupota. Dziękuje bardzo za pomoc, na pewno nigdzie nie ma błędu?