W trójkąt prostokątny wpisano okrąg. Patrycja: Cześć wszystkim. Teść zadania: −w trójkąt prostokątny wpisano okrąg. Punkt styczności okręgu z przeciwprostokątną podzielił ją na odcinki długości 6cm i 4cm. Oblicz pole trójkąta oraz promień wpisanego w niego okrąg. Proszę o pomoc Dziękuje

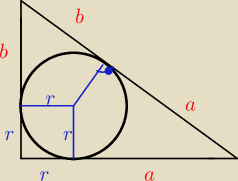
Jack: zatem niech a = 6, b = 4 z pitagorasa (a+r)² + (b+r)² = (a+b)² (6+r)² + (4+r)² = 100 dalej dasz rade.

===: 100=(4+r)²+(6+r)² 100=16+8r+r²+36+12r+r² 2r²+20r−48=0 r²+10r−24=0 Δ=100+96 itd

Jack: promień −> r = ...

	1
Pole trójkąta =		* r * (2a+2b+2r) = r(a+b+r)
	2

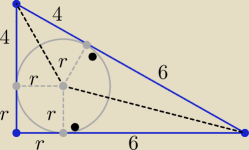
S.O.S.: r>0 (4+r)²+(6+r)²=10² ⇒ ...... r²+10r−24=0 ⇒ (r+12)(r−2)=0 ⇒ r=2 cm

	ab
a=r+6=8 , b=r+4=6 P=		=...........=24 cm2
	2

Metis: η

S.O.S.: "wysyp" jak .... grzybów po deszczu ( albo kleszczy

S.O.S.: lub tak: P= 4+12+8=24 cm²

Patrycja: Dziękuje za pomoc

S.O.S.: Na zdrowie ....