Potrzebuję pilnie pomocy. - nadrobienie zaległości Siwekkk: Witam serdecznie Zadanie brzmi następująco: oblicz promień okręgu wpisanego w trójkąt prostokątny równoramienny, którego wysokość opuszczona na przeciwprostokątną ma długość 4cm. Proszę o rozwiązanie zadanie, bo tylko w ten sposób przez przeanalizowanie i zrobienie innego przykładu jestem w stanie coś zrozumieć. I proszę bez zbędnych komentarzy. Pozdrawiam i z góry dziękuje za pomoc !

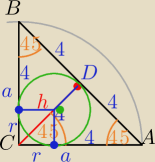Mila: |AC|=|BC|=a 1) CD dzieli AB na połowy 2) W ΔCDA: a²=4²+4² a²=32 a=4√2 r=a−4 r=4√2−4=4*(√2−1) =============== II sposób

	1		1		1
PΔABC=		*a*a=		*a2=		*32=16
	2		2		2

P_ΔABC=p*r, gdzie:

	a+a+8
p=		=a+4=4√2+4
	2

(4√2+4)*r=16 /*(4√2−4) (32−16)*r=16*(4√2−4) r=4√2−4=4*(√2−1) ===============

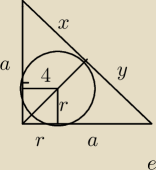Jolanta: h=√x*y jest taki wzór trójkat jst równoramienny czyli x=y 4−√x² 4=x pzeciwprostokątna=8 8=a√2 ( trójkąt o kątach 45,45,90 )

	8
a=		=4√2
	√2

Siwekkk: Dziękuje bardzo za profesjonalne i szybkie odpowiedzi. Miłej nocy życzę, pozdrawiam !