funkcja z parametrem Ola: Dla jakich parametrów m dziedziną funkcji jest zbiór liczb rzeczywistych? f(x)=√x²+(m−3)x+m−3

Jerzy: Warunek: Δ ≤ 0

zef: x²+(m−3)+m−3≥0 Δ≤0

Ola: Dlaczego mniejsza bądź równa 0?

zef: Bo równanie ma być większe lub równe 0

Jerzy: bo wtedy: f(x) ≥ 0

Jerzy: ściślej: trójmian pod pierwiastkiem ≥ 0

Martiminiano: Żeby trójmian kwadratowy nie przyjmował wartości ujemnych (a>0, ramiona w górę)

S.O.S: √a , dla a≥0

Ola: to że trójmian pod pierwiastkiem ma być większy bądź równy 0 to wiem, ale delta mniejsza bądź równa 0? wówczas wynikiem trójmianu będzie liczba urojona czyż nie?

Jerzy: to zależy od parametru m

Jerzy: Bzdurę napisałem ... dla: Δ ≤ 0 trójmian przyjmuje warości nieujemne ze zbioru R

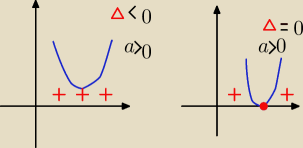
S.O.S: Parabola ramionami do góry bo a=1>0 zatem osiąga wartości nieujemne ≥0 gdy nie ma miejsc zerowych czyli Δ<0 lub ma jedno miejsce zerowe czyli Δ=0 zatem warunkiem na parametr m jest : Δ≤0

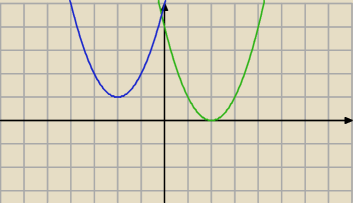
Jerzy: Tu masz przypadek: a > 0 i Δ = 0 (zielony) a > 0 i Δ < 0 ( nieieski)

S.O.S:

S.O.S:

Ola: aaaaaa no oki, a gdyby a było ujemne?

zef: Wtedy m∊∅

Jerzy: dla a < 0 musiało bybyć: Δ = 0

zef: Hmm chwila, nie ! Dajemy przykładowo: −x²+(m−3)x+m−3≥0 Δ>0 m∊<x1;x2>

Jerzy: @zef .... gdy : a < 0 , wtedy: Δ = 0

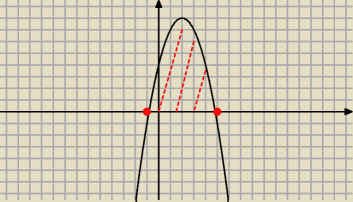
zef: −x²+4x+4 przykładowo 2 miejsca zerowe i odczytujemy to co zaznaczyłem, czy przypadkiem to właśnie tak nie powinno być ?

Jerzy: wtedy dziedziną jest przedział: [x₁,x₂] , a nie zbiór liczb rzeczywistych

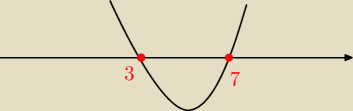
Ola: dobra wyszło mi coś takiego m²−10m+21 ≤0 (to ma być mniejsze bądź równe 0 tak?) wówczas m₁=3 m₂=7 Więc rys. I odpowiedź to <3;7>

zef: Aj no racja, mój błąd