POMOCY!!!! Funkcje1LO: Wykaż że funkcja określona wzorem f od x równa się jedna druga x kwadrat minus jeden jest malejąca w zbiorze prosze o wytłumaczeenie i rozwiązanie nie rozumie tego kompletne a niby funkcje takie łatwe....

Funkcje1LO: w zbiorze (−nieskończoność,0>

zef:

	1
f(x)=		x2−1 Chodzi o tą funkcję ? I nie napisałeś w jakim zbiorze ma być malejąca
	2

Funkcje1LO: f(x) = 1/2 x² −1 wzor funkcji

Funkcje1LO: napisane jest w jakim zbiorze (− ∞ ,0>

zef:

	−b		0
p=		=		=0
	2a		1

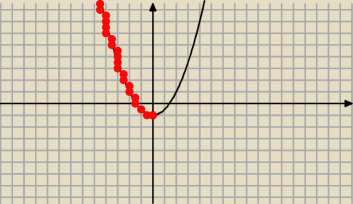
A a>0 więc ramiona do góry czyli najpierw jest malejąca (od minus nieskończoności do pierwszej współrzędnej wierzchołka)

Funkcje1LO: Nadal nie czaje tego ..... a jak by sie zrobiło to zadanie w ten sposób ,że: x1<x2 x1, x2 ⊂(−∞,o> − założenie f(x1)>f(x2) − teza i wyznaczanie różnicy f(x1) − f(x2) ? i dalej nw

zef: Możesz też liczyć inaczej

	x1+x2
p=		jako średnia arytmetyczna dwóch miejsc zerowych.
	2

To jest dłuższa droga bo z wyjściowego równania musisz wyznaczyć oba miejsc zerowe.

Funkcje1LO: skąd to jest : p = −b przez 2a = 0 przez 1 = 0 ? ? ? nie czaje

Mila: zef w I LO badają z definicji.

zef: f(x)=ax²+bx+c − postać ogólna f. kwadratowej W(p,q) współrzędne wierzchołka liczone ze wzorów:

	−b		x1+x2
p=		lub p=
	2a		2

	−Δ
q=f(p) lub q=
	4a

Funkcje1LO: Nie mamy jeszcze f. kwadratowej nie rozumiem kompletnie nic

zef: Nie macie funkcji kwadratowej ale macie zadanie z badania jej monotoniczności ?

Funkcje1LO: mam tak ,że wyszło mi z tych definicji tak : \: x1<x2 x1, x2 ⊂(−∞,o> − założenie f(x1)>f(x2) −teza i wyznaczanie różnicy f(x1) − f(x2) (1/2x1²−1)−(1/2x2²−1) = 1/2 x1² − 1/2 x2² i dalej nie wiem co robic! pomożcie

zef: 1/2x1²−1−1/2x2²+1 1/2x1²−1/2x2² x1=−x2 1/2(−x2)²−1/2x2² 1/2x2²−1/2x2² 0

zef: Zauważ że gdy funkcja ma postać ax²+c gdzie b=0 To ta funkcja ma albo 2 miejsca zerowe (gdy c<0, są one wtedy symetryczne względem osi Y(np 2 i −2)) 1 miejsce zerowe (gdy c=0) lub brak miejsc zerowych gdy c>0

Mila: f(x) jest malejąca w przedziale (−∞,0>⇔dla x₁<x₂ zachodzi nierówność : f(x₁)>f(x₂) i x₁,x₂∊(−∞,0>⇔f(x₁)−f(x₂)>0 1) x₁<x₂⇔x₁−x₂<0 2)

1		1
	x12−1−(		x22−1)=
2		2

	1		1
=		*(x12−x22)=		*(x1−x2)*(x1+x2)>0 bo
	2		2

x₁−x₂<0 (pkt1) i x₁+x₂<0 [jako suma dwóch ujemnych liczb, ( albo jedna ujemna , druga 0)]