Obliczanie delty i rozwiazywanie nierówności Piotrek: Cześć, bardzo proszę o pomoc z tymi dwoma zadaniami : Obliczyć deltę z x²−6x+9 / x−4 =1 x²−6x+5 / x−3 =0 3+4cos(0,5x) =−1 Rozwiąż nierówności: x+3 / x−6 > 0 sinx >= 2sin²x

Janek191:

x2 − 6 x + 9
	= 1 , x ≠ 4
x − 4

x² − 6 x + 9 = x − 4 x² − 7 x + 13 = 0 Δ = 49 − 4*1*13 < 0 − brak pierwiastków

Janek191:

x2 − 6 x + 5
	= 0 , x ≠ 3
x − 3

x² − 6 x + 5 = 0 ( x − 1)*(x − 5) = 0 x = 1 lub x = 5 =============

Mila: 3) 3+4cos(0,5x) =−1 /−3

	x
4cos		=−4 /:4
	2

	x
cos		=−1
	2

x
	=π+2kπ /*2
2

x=2π+4kπ

Jolanta: Δ=b²−4ac x²−6x+9=x−4 x²−7x+13=0 Δ=49−52=−3 x²−6x+5=0 Δ=36−20=16 (x+3)(x−6)>0 x=−3 x=6 parabola ramiona w górę x∊(−∞,−3) v(6,∞)

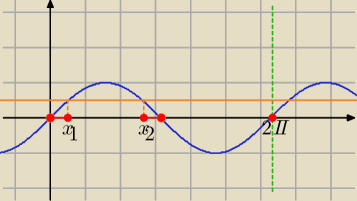
Mila: 5) sinx≥2sin²x 2sin²x−sinx≤0 sinx=t, |t|≤1 2t²−t<0 t(2t−1)≤0

	1
t=0,t=
	2

	1
t∊(0,		)⇔
	2

	1
0≤sinx≤
	2

	π		5π
x∊<0+2kπ,		+2kπ>∪<		+2kπ, π+2kπ>
	6		6

Piotrek: Dziękuję bardzo, pierwszy raz stąd korzystam a tu tak szybko dzięki wielkie

Mila: Obyś skorzystał i nauczył się.