pomocy funkcje Jeffrey: 1. Dana jest funkcja kwadratowa f(x) = 2(x−3)² − 2 Podaj: a) współrzędne wierzchołka paraboli b) zbiór wartości funkcji f c) równanie osi symetrii paraboli d) przedziały monotoniczności funkcji f e) najmniejsza wartość funkcji f f) doprowadź funkcję do postaci ogólnej g) Oblicz jej miejsca zerowe (jeśli istnieją) h) Naszkicuj wykres funkcji 2. Dana jest funkcja kwadratowa podana w postaci iloczynowej: f(x) = − (x−1)(x−3) a) Podaj miejsca zerowe funkcji f b) Oblicz współrzędne wierzchołka paraboli c) Wyznacz współrzędne punktu przecięcia paraboli wykresu funkcji f z osią OY d) Naszkicuj wykres funkcji e) Podaj zbiór wartości funkcji f f) Podaj zbiór argumentów dla których funkcja przyjmuje wartości niedodatnie Proszę o pomoc nie było mnie na lekcji a muszę zrobić to na jutro

zef: Dużo tego, co umiesz z kwadratowej będzie łatwiej.

Jerzy: A co od siebie ?

zef: Zrobisz sam skoro cię na lekcji nie było to Ciebie nakieruję: ax²+bx+c Δ=b²−4ac gdy

	−b−√Δ		−b+√Δ
Δ>0 dwa rozwiązania liczone ze wzoru x1=		x2=
	2a		2a

	−b
Δ=0 Jedno rozwiązanie liczone ze wzoru x=		(to jest zarazem wierzchołek paraboli)
	2a

Δ<0 brak rozwiązań rzeczywistych

	−b		−Δ
A) w(p,q) p=		lub p={x1+x2}{2} q=		lub q=f(p)
	2a		4a

B)Zw jest zawsze dla a>0(ramiona do góry) <q;+∞) gdy a<0 (−∞;q> C)x=p d)Z rysunku odczytasz e)Najmniejsza wartość jest wtedy tylko gdy a>0 i to jest q f)Podnieś to co w nawiasie do kwadratu i uporządkuj g)Napisałem wcześniej h) Chyba potrafisz

Jeffrey: dzięki zef już sobie poradze

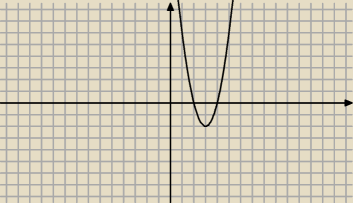
zef: Nie ma sprawy, tutaj jeszcze dorzucam rysunek z którym łatwiej będzie ci się robiło te podpunkty.