Jak się to rozwiązuje/?
keraj: Rozwiąż równanie
sinx=sinx(x− π)+1
16 maj 20:07
Jerzy:
Najpierw to porządnie zapisz
16 maj 20:08
Jerzy:
| | 1 | |
sinx = sin(x−π) + 1 ⇔ sinx = sin[−(π−x)] ⇔ sinx = −sinx + 1 ⇔ 2sinx = 1 ⇔ sinx = |
| |
| | 2 | |
16 maj 20:11
keraj: nic z tego nie rozumiem
16 maj 21:01
Jerzy:
a konkretnie czego ?
16 maj 21:01
keraj: Tej części sinx = sin(x−π) + 1 ⇔ sinx = sin[−(π−x)]
16 maj 21:11
zef: sin[−(π−x)]=sin[−(x−π)]
16 maj 21:13
Jerzy:
(x − π) = − (π − x)
sin(π − x) = sinx
sin(−x) = − sinx
teraz jaśniej ?
16 maj 21:13
Jerzy:
a może tak:
sin[−(π − x)] = −sin(π − x) = − sinx
16 maj 21:15
keraj: ok, ale dlaczego ten sinπ znika
16 maj 21:23
Jerzy:
sin(π − x) = sinx ( wzór redukcyjny )
16 maj 21:23
zef:
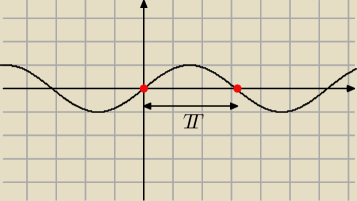
Przesunięcie o π w prawo nic nam nie zmienia
16 maj 21:24
keraj: dzięki ; ) już jaśniej
16 maj 21:31