Rozwiąż układ równań i podaj jego interpretację geometryczną
Pablo: Jak to wgl policzyć?
a)
{ (x+y)(x+y−1)
{ x2 + y2 + 2y = 0
b)
{ x2 − 2x − y = 0
{ (x−1)2 + y2 = 13
15 maj 19:55
Pablo: tam w a) pierwsze równanie jest równe 0
15 maj 19:56
zef: (x+y)(x+y−1)=...
15 maj 19:56
6latek :
b)
−y= −x
2+2x to y= x
2−2x
wstawiamy do drugie równania
(x−1)
2+(x
2−2x)
2=13
rozwiąż to równanie (wylicz x
sy i potem wstaw je do 1 równania czyli y=x
2−2x i wylicz y
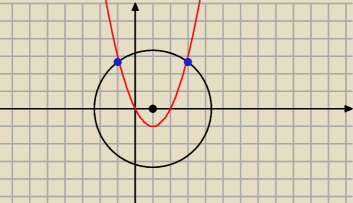
Graficznie
y=x
2−2x to parabola
(x−1)
2+y
2=13 to okrag o srodku S=(1,0) i promieniu r=
√13
15 maj 20:03
Pablo: jak mam rozwiązać to równanie?
(x−1)2+(x2−2x)2=13
z tego wychodzą potęgi do 4, 3 i 2
15 maj 20:09
6latek :
a) graficznie
Pierwszwe równanie (x+y)(x+y−1)=0 przedstawia dwie proste \x+y=0 to y=−x a także prosta
x+y−1=0 to y=−x+1= 1−x
Drugie równanie przedstawia okrag
x
2+y
2+2y=0 to (x−0)
2+(y+1)
2−1=0 to (x−0)
2+(y+1)
2=1 o srodku S(0.−1) i promieniu r=1
15 maj 20:13
6latek : Niech wychodzą takie potęgi .
Policzyles to ?
15 maj 20:15
Pablo: x
2−2x+1+x
4−4x
3+4x
2=13 i co dalej?

nie miałem wcześniej takich równań nie wiem jak to rozwiązać

15 maj 20:23
Mila:
b)
x
2 − 2x − y = 0
(x−1)
2 + y
2 = 13
−−−−−−−−−−−−−−−−−−
(x−1)
2−1−y=0
(x−1)
2+y
2=13
−−−−−−−−−−−−−−−−−−−−−
odejmujemy stronami
−1−y−y
2=−13
y
2+y−12=0
Δ=1+48=49
| | −1−7 | | −1+7 | |
y1= |
| lub y2= |
| |
| | 2 | | 2 | |
y
1=−4 lub y
2=3
podstawiamy do pierwszego równania
x
2 − 2x − (−4) = 0 lub x
2−2x−3=0
dokończ.
15 maj 20:23
Pablo: { x = −1
{ y = 3
lub
{x = 3
{y = 3
?
15 maj 20:28
6latek : Milu 
możesz zrobić to zadanie nr 1 algebraicznie ?
Nie wiem czy robic tutaj jakies podstawienie za x+y=u ?
15 maj 20:30
Pablo: jest dla mnie jakaś nadzieja żebym zdał maturę rozszerzoną z matmy jak jestem w pierwszej
klasie liceum i takie coś sprawia mi problem

? czy już powinienem się poddać?
15 maj 20:36
6latek : Oczywiscie ze sie nie poddawaj .
Ty jestes w 1 klasie . Podejrzewam ze niektorzy maturzysci by mieli z tym klopoty
15 maj 20:41
Pablo: dzięki za pocieszenie

czyli jest nadzieja, w te wakacje postaram się wszystkie zaległości
nadrobić i zrozumieć od podstaw jak najwięcej bo geometria analityczna jest dla mnie problemem
15 maj 20:47
6latek : x
2−2x−(−4)=0
x
2−2x+8=0
Δ= 4−4*1*8=4−32=−28 <0 brak rozwiazan
x
2−2x−3=0
Δ=4+12=16 >0
Wiec masz dwie pary liczb spelniajacych ten uklad (3,3) oraz (−1,3)
15 maj 20:48
6latek : Wbrew pozorom to nie sa takie latwe zadania .
Trzeba sie troche natrudzic zeby je rozwiazac . Trzeba znac sposoby
15 maj 20:52
Mila:
Zaraz zrobię pierwsze, oglądam koncert.
15 maj 20:56
Pablo: Bardzo dziękuję Wam za wsparcie i pomoc

15 maj 21:00
Mila:
Pablo W pierwszej klasie nie miałeś jeszcze równań kwadratowych
to dlatego to trudne dla Ciebie.
Dokończenie b) bez delty
x
2−2x−3=0⇔
(x−1)
2−1−3=0
(x−1)
2=4
x−1=2 lub x−1=−2
x=3 lub x=−1
Mamy pary
x=−1 i y=3
x=3 i y=3
a)
(x+y)(x+y−1) =0
x
2 + y
2 + 2y = 0
x+y=0 lub x+y−1=0 ( suma prostych)⇔
y=−x lub y=−x+1
I)
y=−x podstawiamy do drugiego rownania:
x
2+(−x)
2+2*(−x)=0⇔
2x
2−2x=0 ( takie równania już miałeś)
2x*(x−1)=0
x=0 lub x=1
Mamy pary:
x=0 i y=0
x=1 i y=−1
II)
y=−x−1 podstawiamy do równania : x
2 + y
2 + 2y = 0
x
2+(−x+1)
2+2*(−x+1)=0
x
2+(−x+1)
2−2x+2=0
x
2+x
2−2x+1−2x+2=0
2x
2−4x+3=0 /:2
| | 1 | |
(x−1)2=− |
| brak rozwiązań, bo (x−1)2≥0 dla x∊R |
| | 2 | |
Pablo rozwiązuj zadania ze zbioru dla klas I.
Zaraz podam Ci zestawy na Twoim poziomie .
15 maj 21:15
15 maj 21:18
6latek : dziekuje CI
Milu 
Tak samo mi wyszlo graficznie .
czyli kratki mi wyszly kwadratowe nie prostokatne ( zawszse sie smiala z tego
Eta 
15 maj 21:19
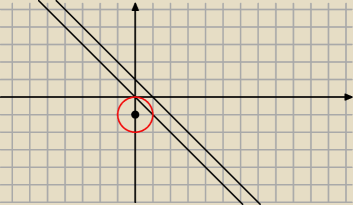
P.: x²−4x−2y=0
2x+y−2=0
8 kwi 12:55
Chińska podróba 6-latka: to możesz chytrze zrobić
zauważ że z drugiego równania
2x+y=2 czyli 4x+2y=4 , a więc −4x−2y=−4
podstawiasz do pierwszego i masz x2−4=0 czyli x=−2 lub x=2
i odpowiednio y do każdego z nich policz y=2−2x
8 kwi 12:59
chichi:
x
2−4x−2(2−2x)=0
x
2−4=0
(x−2)(x+2)=0
lub
8 kwi 13:02
Get it back:
8 kwi 13:14
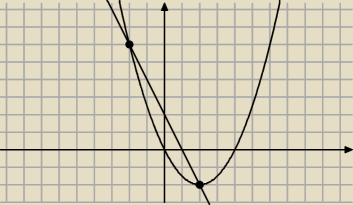
 b)
−y= −x2+2x to y= x2−2x
wstawiamy do drugie równania
(x−1)2+(x2−2x)2=13
rozwiąż to równanie (wylicz xsy i potem wstaw je do 1 równania czyli y=x2−2x i wylicz y
Graficznie
y=x2−2x to parabola
(x−1)2+y2=13 to okrag o srodku S=(1,0) i promieniu r=√13
b)
−y= −x2+2x to y= x2−2x
wstawiamy do drugie równania
(x−1)2+(x2−2x)2=13
rozwiąż to równanie (wylicz xsy i potem wstaw je do 1 równania czyli y=x2−2x i wylicz y
Graficznie
y=x2−2x to parabola
(x−1)2+y2=13 to okrag o srodku S=(1,0) i promieniu r=√13
 a) graficznie
Pierwszwe równanie (x+y)(x+y−1)=0 przedstawia dwie proste \x+y=0 to y=−x a także prosta
x+y−1=0 to y=−x+1= 1−x
Drugie równanie przedstawia okrag
x2+y2+2y=0 to (x−0)2+(y+1)2−1=0 to (x−0)2+(y+1)2=1 o srodku S(0.−1) i promieniu r=1
a) graficznie
Pierwszwe równanie (x+y)(x+y−1)=0 przedstawia dwie proste \x+y=0 to y=−x a także prosta
x+y−1=0 to y=−x+1= 1−x
Drugie równanie przedstawia okrag
x2+y2+2y=0 to (x−0)2+(y+1)2−1=0 to (x−0)2+(y+1)2=1 o srodku S(0.−1) i promieniu r=1
 nie miałem wcześniej takich równań nie wiem jak to rozwiązać
nie miałem wcześniej takich równań nie wiem jak to rozwiązać
 możesz zrobić to zadanie nr 1 algebraicznie ?
Nie wiem czy robic tutaj jakies podstawienie za x+y=u ?
możesz zrobić to zadanie nr 1 algebraicznie ?
Nie wiem czy robic tutaj jakies podstawienie za x+y=u ?
 ? czy już powinienem się poddać?
? czy już powinienem się poddać?
 czyli jest nadzieja, w te wakacje postaram się wszystkie zaległości
nadrobić i zrozumieć od podstaw jak najwięcej bo geometria analityczna jest dla mnie problemem
czyli jest nadzieja, w te wakacje postaram się wszystkie zaległości
nadrobić i zrozumieć od podstaw jak najwięcej bo geometria analityczna jest dla mnie problemem

 Tak samo mi wyszlo graficznie .
czyli kratki mi wyszly kwadratowe nie prostokatne ( zawszse sie smiala z tego Eta
Tak samo mi wyszlo graficznie .
czyli kratki mi wyszly kwadratowe nie prostokatne ( zawszse sie smiala z tego Eta 
