zadanie trudne
Rafal44: Na półokręgu, którego średnicą jest odcinek AB, obrano punkt S (różny od punktów A i B),
którego rzutem prostokątnym na prostą AB jest punkt C. Następnie narysowano okrąg styczny do
prostych SC i AB i mający jeden punkt wspólny z łukiem AS. Wykaż, że trójkąt, którego
wierzchołkami są punkty S, B i punkt styczności narysowanego okręgu z prostą AB, jest
równoramienny.
15 maj 19:03
Janek191:
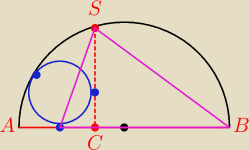
15 maj 19:29
Rafal44: up
15 maj 20:19
jc: Oznacz punkt styczności małego okręgu z odcinkiem AC literą Q.
Mamy BQ2 = 2 R BC = BS2, gdzie R jest promieniem dużego okręgu.
Aby to pokazać wystarczy kilka razy skorzystać z Tw. Pitagorasa.
Dorysuj odcinek łączący środek dużego okręgu z punktem styczności
małego okręgu z dużym. Odcinek ten przechodzi przez środek małego okręgu.
15 maj 21:36
Rafal44: Dziękuję za pomoc, aczkolwiek to, to ja wiedziałem na początku. Potrzebuję obliczeń, bo mój
umysł jest w jakimś stanie zaćmienia.
PS. Zadanie nie jest w ramach pracy domowej itd.
16 maj 18:07
reindeer: dlaczego odcinek łączący środek dużego okręgu z punktem styczności
małego okręgu z dużym przechodzi przez środek małego okręgu? Twierdzenie Pitagorasa wystarczy
zastosować w trójkątach SCQ SCB i SQB czy jeszcze gdzieś?
22 mar 12:04
wredulus_pospolitus:
co do pierwszego pytania
1. jeżeli dwa okręgi są styczne do siebie (wewnętrznie lub zewnętrznie) w punkcie P, to znaczy
że ... oba okręgi są styczne w punkcie P DO TEJ SAMEJ PROSTEJ.
2. i to właśnie powoduje, że środki okręgów będą leżały na ten samej prostej (która jest
prostopadła do stycznej) przechodzącej przez punkt P.
22 mar 12:53
reindeer: Dzięki, teraz to jest jasne. A z tym Pitagorasem to te trzy trójkąty wystarczą czy coś gdzieś
dorysować? Bo nie wychodzi mi nic...
22 mar 14:29
Mila:
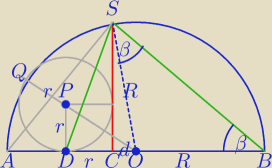
∡ASB=90
o
1)
| | d+R | | BS | |
stąd : |
| = |
| ⇔|BS|2=2R(d+R) |
| | |BS| | | 2R | |
2)
|BD|=(r+d)+R
wΔDOP: |OP|=R−r
(R−r)
2=r
2+(r+d)
2
(r+d)
2=R
2−2rR+r
2−r
2
(r+d)2=R2−2Rr
|BD|
2=(r+d)
2+2R(r+d)+R
2⇔ |BD|
2=
R2−2Rr+2Rr+2Rd+R
2
|BD|
2=2R
2+2Rd
|BD|
2=2R(R+d)=|BS|
2
|BD|=|BS|
ΔBDS− Δrównoramienny
==================
24 mar 14:52

 ∡ASB=90o
1)
∡ASB=90o
1)