Udowodnij tożsamość trygonometryczną. Maciek4x: Trygonometria 1.Udowodnij tożsamość trygonometryczną. a) (1+cosx)(1−cosx)=sin²x b) cosx×sin²x+cos³ x=cosx c) 1−2sinx×cosx=(sinx−cosx)² d) cos²x+tg²x×cos²x=1 2. Oblicz wartości pozostałych funkcji trygonometrycznych kąta x https://zapodaj.net/803bd12634196.jpg.html Prosił bym o wytłumaczenie zadania 1 oraz 2 oraz 4

Krzysiek: (1+cosx)(1−cosx)= 1−cos²x = ile ?

Krzysiek: (sinx−cosx)²= sin²x−2sinxcosx+cos²x =

Krzysiek: Jak się laskawie odezwiwesz to być może pomoge w dalszych przykładach

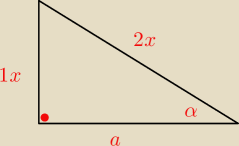
Jack: zadanie 2. Pierwszy sposób : Robisz układ równań, gdzie pierwszym równaniem jest jedynka trygonometryczna, a drugim dana z zadania. np. podpunkt a) {sin²x + cos²x = 1

	1
{sinx =
	2

podstawiasz do jedynki ten sinus, otrzymujesz cosinus, a potem tangens x = sinx / cosx Drugi sposób (który ja osobiście preferuje): Rysujemy trójkąt prostokątny i oznaczamy z danych z zadania np. podpunkt a)

	1
sinx =
	2

zatem oznaczamy boki 1x, 2x (iksy muszą być, bo sinus = 1/2 ale boki mogą być też 2/4, 3/6 itd, wiec wielokrotności tego.) Obojętne gdzie zaznaczysz kąt alfa, bylebyś dobrze zaznaczył funkcję. zaznaczamy boki, 1x, 2x bo sinus = 1/2. z pitagorasa obliczamy trzec bok : (2x)² − (1x)² = a² −>> a = x√3 no i wyznaczamy pozostale funkcje.

	a		x√3		√3
np. cosinus x =		=		=
	2x		2x		2

Maciek4x: Krzysiek nie rozumiem pytania

Krzysiek: Tego z 16:56? sin²x+cos²x=1 ⇒1−cos²x= ile?

Maciek4x: Ale co ile ?

Krzysiek: Jack po co ten układ do tego ? jeśli ma dane sinx to

	3		√3
cosx= √1−sin2x = √		=
	4		2

	sinx		1		2		2		2√3
tgx=		=		*		=		=		= skroc to
	cosx		2		√3		2√3		6

	1
ctgx=
	tgx

Krzysiek: czy ja piszse po chińsku ? Przeciez postawiłem znak rownosci ,czyli ile to się rowna

Krzysiek:

	sin2x
d) cos2x+tg2x*cos2x= cos2x+		*cos2x= cos2x+sin2x= ile ?
	cos2x

Jack: Krzysiek to co napisales wynika z jedynki trygonometrycznej, czyli wlasnie z tego ukladu. Ja pisze tak, zeby wiedzial skad jest co, bo raczej nie jest osoba ktora odrazu widzi takie rzeczy

Krzysiek: Tak wlasnie jest Potem majac dany sinx nie policzy tgx bo nie ma cosinusa Pytam się po co cosinus ?

	sinx		sin
Przeciez tgx=		=		i już jest tangens policzony ( bez cosinusa
	cosx		√1−sin2x

Krzysiek:

	√1−cos2x
Tak samo masz cosx to tgx=
	cosx

Powinni to w szkole uczyc anie jakies układy