Obliczanie punktu w prostej równoległej James: Mam problem z zadaniem : Punkt (2,t) leży na prostej równoległej do prostej o równaniu

	3
y=		x + 5 i przechodzącej przez punkt (6,4). Oblicz t.
	2

Metis: Prosta równoległa do danej prostej:

	3
y=		x+b
	2

Znajdź b podstawiając podany punkt. poźniej rozwiąż f(2)=t

James: No tak tylko że ten punkt ma niewiadomą bo jest to (2,t) i jak mam obliczyć z tego b ? Skoro wyjdzie z tego że b= t−3 co później przy wyliczaniu skróci się.

Metis: 4=3/2*6+b oblicz b

Krzysiek: Metis po co b ? przecież równanie prostej przechodzącej przez dany punkt (x₀ y₀) jest takie y= a(x−x₀)+y₀

	3
y=		(x−6)+4
	2

y= 1,5x−9+4 y=1,5x−5 Przeciez na studiach nie będziesz liczyl b.

Metis: Przecież to to samo Wiem, że na studiach nie będę przypominał sobie jakiegoś bezużytecznego wzoru, na prostą przechodzącą przez dany punkt skoro mogę go wyprowadzić. Z resztą o czym rozmawiamy.

Krzysiek: No wlasnie Metis o tym ze to robisz .

Mila: Ja zawsze pamiętam wzór prostej y=ax+b. Metoda Metisa jest w porządku.

Krzysiek: dzień dobry Milu Pozdrawiam Ale czy w szkole nie powinni uczyc wzoru na prosta przechodzaca przez dwa punktyA=(x₁,y₁) i B=(x₂,y₂) w postaci

y2−y1		y−y1
	=		i wytlumaczyc ze po lewej stronie jest to wspolczynnik
x2−x1		x−x−1

kierunkowy tgα=a prostej . Lepiej jest ich uczyc przez układ rownan , a później nie wiedza co to jest tgα

Krzysiek: poprawie

	y−y1
=		ma być
	x−x1

S.O.S: jeżeli x₁≠x₂

Krzysiek: To oczywiste . Tez pozdrawiam

Mila: Jeżeli rozumiesz wzór y=ax+b to nie ma kłopotu.

James: Te dwa punkty leżą na dwóch różnych prostych więc jak mogę wyliczyć współczynnik b dla innej prostej i podstawić go do drugiej ? Skoro te dwie proste są do siebie równoległe to nie mogą mieć wspólnych punktów.

Mila:

	3
Mają taki sam wsp. kierunkowy a=
	2

	3
k: y=		x+5 dana prosta
	2

m||k⇔

	3
m: y=		x+b i P=(6,4)∊m⇔ spełnia równanie tej prostej, obliczymy b
	2

	3
4=		*6+b⇔b=−5
	2

	3
m: y=		x−5
	2

	3
y=		*2−5=−2 ⇔t=−2
	2

A=(2,−2)

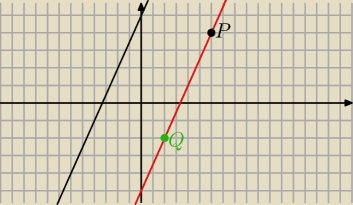
Krzysiek : czarna to prosta y=1,5x+5 Czerwona to prosta y=1,5x−5 i jest ona rownolegla do prostej y=1,5x+5 i przechodzi przez punkt (6,4) Masz znaleźć taki punkt oznaczmy go przez Q który z warunkow zadania lezy na prostej czerwonej Wiemy o nim ze jego wspolrzedna x_owa =2 i y_owa =t WLasnie musimy t wyliczyć Wiemy ze jeśli punkt należy do prostej to spelnia jej równanie Rownanie czewronej prostej jest takie y=1,5x−5 wstawiamy za y t do rownia tej prostej a za x =2 t=1,5*2−5 t=3−5=−2 Czyli ten punkt Q który będzie miał takie wspolrzedne Q=(2,−2) Sprawdz na rysunku czy się zgadza

James:

	3
Z treści zadania rozumiem ze punkt P(6,4) należy do prostej o wzorze y=		x+5 więc na twoim
	2

rysunku do należy do prostej k więc jak może jednocześnie należeć do prostej m ? Tak przynajmniej jak dla mnie wynika z treści zadania.

6latek :

	3
Z treści zadania wcale nie wynika ze punkt P należy do prostej y=		x+5
	2

Przeczytaj jeszcze raz zadanie

Mila:

	3
P(6,4)∉prostej y=		x+5 bo nie spełnia jej równania, zresztą to widać na rysunku.
	2

	3
4≠		*6+5
	2

6latek : Milu Kolega pewnie już zrezygnowal

James: No czytam i jak dla mnie to właśnie to oznacza skoro jakiś punkt leży na prostej równoległej do jakiejś tam i przechodzącej przez punkt jakiś tam. Skoro jest inaczej to nie mam żadnego problemu z tym zadaniem

Mila: Zadanie powinno być jaśniej sformułowane, ale przecież możesz łatwo sprawdzić, że P(6,4) nie leży na danej prostej, tylko na tej której szukasz.