Planimetria , długość okręgu i pole koła zielonooka: Punkty A, B leżą na okręgu o średnicy 10 cm , |AB| = 5 cm . Ile jest równa długość łuku AB?

Krzysiek: https://matematykaszkolna.pl/strona/476.html

Mariusz: Odcinek |AB| tworzy z promieniami trójkąt równoboczny więc kąt między promieniami

	π
zawierającymi punkty A oraz B wynosi
	3

Jeśli nie pamiętasz wzoru na długość wycinka kołowego to może uda ci się go wyprowadzić całką

Mariusz: * długość łuku

Mariusz: x(t)=rcos(t) y(t)=rsin(t) x'(t)=−rsin(t) y'(t)=rcos(t) √(x'(t))²+(y'(t))²=√r²sin²(t)+r²cos²(t)=√r²(sin²(t)+cos²(t)) =√r²=r ∫_t1^t₂rdt =r∫_t1^t₂dt =r(t₂−t₁)

	xB
t2=arccos(		)
	5

	xA
t1=arccos(		)
	5

Tutaj

	π
t2−t1=
	3

zatem

	5
l=		π
	3

zielonooka: A jakoś prościej? Nie wiem o co w tym chodzi . Wiem że S= 10 cm , odcinek 5 i musze teraz wyliczyc dlugosc łuku i mam wzór L = alfa/ 360 * 2 pi * r ale ile bedzie r ? I do czego potrzebuje S ? Pomocy

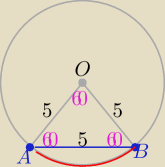
S.O.S: Dane :2r=10 ⇒ r=5 i |AB|=5=r Uwzględniając treść zadania to ΔABO jest równoboczny o boku długości 5 |∡AOB|=60^o −−− miara kąta środkowego o łuku AB

	60o		1		5
zatem |łuku AB|=		*wπr=		*10π= ...=		π
	360o		6		3

S.O.S: w ostatnim zapisie zamiast w ma być oczywiście : 2πr