Parametr Pati18773: Dla jakiej wartości parametru m€R f (c)=x²+(m+1)x+3−m suma odwrotności kwadratów dwóch różnych miejsc zerowych funkcji f (x) jest większa od 1. Zastanawiam się nad warunkami zadania. Stwierdziłam że 1. Δ>0 2. x₁×x₂ <0 To wystarczy ?

ICSP: Wystarczy Δ > 0

ICSP: Plus oczywiście zadany warunek :

1		1
	+		> 1
x12		x22

Krzysiek: ! warunek tak Natomiast suma odwrotności kwadratow dwocg roznych miejsc zerowych to

1		1		x22		x12
	+		=		+		=
x12		x22		x12*x22		x12*x22

	x22+x12		x12+x22
		=
	x12*x22		x12*x22

x₁²+x₂²= (x₁+x₂)²−2x₁*x₂ natomiast x₁²*x₂²= (x₁*x₂)² Widzisz wzory Vieta ?

Pati18773: Wyszło że m₁=−3−2√5 i m₂=−3+2√5

Pati18773: Niee

Pati18773: Znaczy tak xd

Krzysiek: Osobiscie mi się nie chce tego liczyc . Dawaj obliczenia

Pati18773: Tylko dlaczego x12+x22= (x1+x2)2−2x1*x2?

Pati18773: x₁²+x₂²= (x₁+x₂)²−2x₁*x₂ *

Krzysiek: Wzor skroconego mnoznia (a+b)²= a²+2a*b +b² Teraz żeby dostać a²+b² musisz od (a+b)² odjąć 2a*b

Pati18773: 1. Δ>0 a=1 b=m+1 c=3−m (m+1)²−4×1×(3−m)>0 m²+2m+1−12+4m>0 m²+6m−11>0 Δ=80 √Δ=4√5 m₁=−6−4√5/2=−3−2√5 m₂=−3+2√5

Pati18773: I teraz mam te m podstawic za x?

Krzysiek: masz tak m>0 i Δ>0 wiec napisz do jakiego przedzialu należy m Ramiona tej paraboli będą skierowane w gore

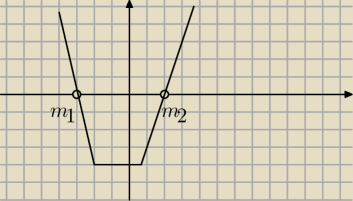
Krzysiek: gdzie jest m>0 ?

Pati18773: No to mam ze m€(−∞ ; −3−2√5) U ( −3+2√5 ; +∞)

Krzysiek: No dobrze Tylko zapisz ze −3+2√5= 2√5−3 (lepiej wygląda bo dodawanie jest przemienne Masz 1 warunek wyznaczony Teraz wyznaczaj drugi

Pati18773: Wyszlo ze x₁+x₂=1−m i x₁x₂=3−m

Pati18773: m²−5/m²−6m+9 >1 Mogę pomnożyć przez mianownik ?

Krzysiek:

	1		1
No to		+		>1
	x12		x22

(x1+x2)2−2x1*x2
	>1
(x1*x2)2

podstawiaj i licz

Jack: m²−6m+9 = (m−3)²

Pati18773: To wiem xd

Krzysiek: Wyszlo CI tak

m2−5
	>1
m2−6m+9

Możesz pomnozyc przez mianownik jeśli wyrzucisz m=3 z dziedzny bo wtedy dostaniesz dzielenie przez 0

Pati18773: No to tak: m€(14/6;3)U (3;+∞) Po wyznaczeniu wspólnej części wyszlo tak samo m€(14/6;3)U (3;+∞)

Krzysiek: powinno być dobrze