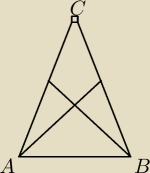
Geometria matematyk: Zadanie: W trójkącie równoramiennym ABC o podstawie AB środkowe poprowadzone z wierzchołków A i B są prostopadłe. Oblicz sinus kąta ACB. Narysowałem trójkąt który jest u góry i nie wiem jak o ruszyć

jc: 3/5 Niech D będzie środkiem boku AC. Podziel odcinek AB na 4 równe części. W 1/4 od A zaznacz punkt E. sin ACB/2 = sin ADE = AE/AD = 1/√10, ED = EB (dlaczego?) cos ACB/2 = cos ADE = DE/AD = 3/√10 sin ACB = 2 sin ACB/2 * cos ACB/2 = 3/5 Na pewno można dużo ładniej, jak masz czas i siły o tej porze, to pomyśl! Albo czekaj, aż przyjdzie Mila

matematyk: trochę za bardzo to dla mnie skomplikowane :v

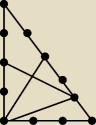jc: Trochę krzywo. W trójkącie o bokach 3,4,5 widzisz Swój trójkąt. Sinus odczytujesz z rysunku = 3/5.

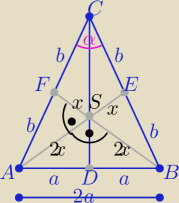Eta: 1/ środkowe dzielą się w stosunku 2:1 licząc od wierzchołka |AS|=|BS|=2x, |FS|=|ES|=x , x>0 2/ z tw. Pitagorasa : b²=5x² i 4a²=8x² ⇒ b=√5x to 2b= 2√5x i a²=2x² |DC|²=h²= 20x²−2x² ⇒ h= 3√2x

	1		1
P(ABC)=		*a*h = ......= 6x2 i P(ABC)=		|AC|*|BC|*sinα
	2		2

⇒ 2b²*sinα=6x²

	3
10x2*sinα=6x2 ⇒ sinα=
	5

Mila: Środkowe trójkąta dzielą się w stosunku 2:1 licząc od wierzchołka ΔSDB− Δprostokątny równoramienny |CD|=h=3a W ΔADC:

	a		1
tgγ=		=
	3a		3

sinγ		1
	=
cosγ		3

	1
sinγ=		cosγ
	3

cosγ=3sinγ sin²γ+(3sinγ)²=1 10sin²γ=1

	1
sinγ=
	√10

	3
cosγ=
	√10

	1		3
sin(2γ)=2*sinγ*cosγ=2*		*
	√10		√10

	6		3
sin(2γ)=		=
	10		5