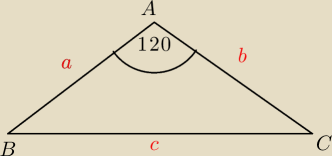
 Nazwijmy boki jak na rysunku. (a≤b≤c oraz a,b,c>0)
Skoro tworza ciag arytm. to
2b = a + c
oraz z tw. cos.
c2 = a2 + b2 − 2ab cos 120
Nazwijmy boki jak na rysunku. (a≤b≤c oraz a,b,c>0)
Skoro tworza ciag arytm. to
2b = a + c
oraz z tw. cos.
c2 = a2 + b2 − 2ab cos 120
| 1 | ||
cos 120 = cos (180−60) = − cos 60 = − | ||
| 2 |
| 1 | ||
c2 = a2 + b2 − 2ab * (− | ) = a2 + b2 + ab | |
| 2 |
| 3 | ||
lub 3b = 5a −−−> a = | b | |
| 5 |
| 3 | 7 | |||
c = 2b−a = 2b − | b = | b | ||
| 5 | 5 |
| 3 | 7 | ||
b , b , | b | ||
| 5 | 5 |