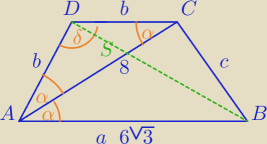
Trapez Pati18773: Dany jest trapez ABCD o podstawach AB I CD w którym AB=6√3 i AD=DC. Przekątna AC ma długość 8 i tworzy z podstawą AB kat o mierze 30'. Przekątna trapezu przecinają się w punkcie S. Oblicz: a) długości ramion trapezu b) stosunek pola trójkąta ABS do pola trójkąta CDS Jedno takie już wyliczylam 2√7 a reszty nie wiem

Pati18773: Jedno ramię *

Mila: 1) α=30^o ΔACD−Δrównoramienny δ=180−2*30=120^o 8²=b²+b²−2*b*b*cos(120^o) 64=2b²+b² 3b²=64

	8		8√3
b=		=
	√3		3

c=2√7

	a		6√3		9
2)ΔABS∼ΔCDS w skali k=		=		=
	b		8√3   3		4

Stosunek pół figur podobnych jest równy kwadratowi skali podobieństwa

PΔABS		9
	=(		)2=81:16
PΔCDS		4