matura ***: Zrobi ktoś to ostatnie zadanie z matury rozszerzonej z matematyki? Z góry dzięki

Metis:

	1
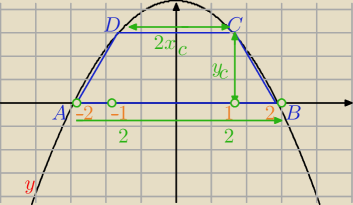
Parabola o równaniu y=2−		x2 przecina oś Ox układu współrzędnych w punktach
	2

A =(−2,0) i B = (2,0). Rozpatrujemy wszystkie trapezy równoramienne ABCD, których dłuższą podstawą jest odcinek AB, a końce C i D krótszej podstawy leżą na paraboli. Wyznacz pole trapezu ABCD w zależności od pierwszej współrzędnej wierzchołka C. Oblicz współrzędne wierzchołka C tego z rozpatrywanych trapezów, którego pole jest największe. Niech C=(x_c , y_c)

	|AB|+|CD|
PABCD=		*h
	2

|AB|=4 |CD|=2x_c h=y_c Widzi się ,że x_c∊(0,2)

	1
Wiemy, że C należy do paraboli o równaniu y=2−		x2, więc :
	2

	1
C=(xc, 2−		xc2)
	2

	1
Zatem h=2−		xc2
	2

	4+2xc		1
P(xc)=		*(2−		xc2 )
	2		2

	1
P(xc)=−		x3−xc2+2xc+4
	2

	3
P'(xc)=−		xc2−2xc+2
	2

Szukamy min.

	3
P'(xc)=0 ⇔ −		xc2−2xc+2=0
	2

√Δ=4

	2
xc1=−2 v xc2=
	3

x_c1 nie należy do (0,2)

	2
Badamy P'(xc)>0 i P'(xc)<0 i wnioskujemy, że w xc=		mamy maksimum.
	3

	2		16
Zatem C=(		,		)
	3		9

Metis: *Szukamy maks.

===: a co w nim trudnego Dłuższa podstawa 4 Krótsza 2|x_c| Wysokość f(x_c) Wzór na pole trapezu Badanie funkcji ...

Mila: Oś y jest osią symetrii trapezu. Rozważamy przypadek gdy x∊(0,2).

hehe: mila, proszę zajrzyj do mnie

pultasek: czemu x∊(0,2) ?

ite: Punkt C został tak wybrany, że należy do pierwszej ćwiartki ukł.współrzędnych i leży na paraboli ("przesuwa się") po niej. Warunek Metisa "widzi się" wynika stąd, że pierwsza współrzędna punktu C musi się zawierać między pierwszymi współrzędnymi osi OY i pkt B.