geometria przestrzenna ppp: W graniastosłupie prawidłowym czworokątnym suma długości jego krawędzi jest równa 68 cm, a pole powierzchni całkowitej 190 cm².Oblicz długość krawędzi graniastosłupa.

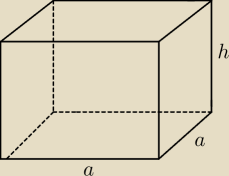
Jack: Rysunek to podstawa. Na maturze za sam rysunek jest chyba jakis punkt

Jack: Wszystkich krawedzi 8a + 4h = 68 P_c = 2a² + 4ah = 190 z pierwszego rownania 8a + 4h = 68 // : 4 2a + h = 17 −>> h = 17 − 2a z drugiego 2a² + 4ah = 190 a² + 2ah = 95 a² + 2a(17−2a) = 95 a² + 34a − 4a² = 95 −3a² +34a − 95 = 0 delta...

ppp: Δ=34²−4*(−3)*(−95)=1156−1140=16 √Δ=4

ppp: x₁=5 x₂=¹⁹₃

ppp: I co dalej?

Janek191: a = 5, więc h = 17 − 2*5 = 7 lub

	1		2		1
a = 6		, więc h = 17 − 12		= 4
	3		3		3

Odp. a = 5, h = 7 lub

	1		1
a = 6		, h = 4
	3		3