wyznacz styczną ja: Wyznacz równania stycznych do okręgu (x − 1)² + (y − 1)² = 4 przechodzących przez punkt P(−1,−3) Wyznaczyłam jedno równanie stycznej współczynnik a będzie wtedy wynosił 3/4 Jednak ponoć powinna być jeszcze jedna prosta, tyle że nie mam pojęcia jak ją wyznaczyć. zadanie rozwiązywałam ze wzoru na odległość środka okręgu od tej stycznej, która ma się równać promieniowi. ktoś pomoże?

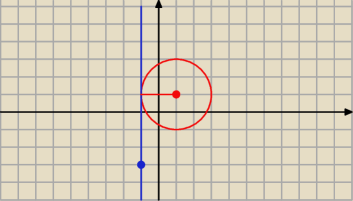
Janek191: Równanie tej drugiej prostej : x = − 1

ja: ale jak to jakoś tak obliczeniowo wyznaczyć?

Janek191: r = 2 S₁ = ( 1 − 2, 1) = ( − 1, 1) P = ( − 1, − 3) więc oba punkty maja równe odcięte, zatem prosta S₁ P ma równanie x = − 1

ja: dziękuję bardzo

Mariusz: F(x,y)=(x−1)²+(y−1)²−4

δ F
	=2(x−1)
δ x

δ F
	=2(y−1)
δ y

	x0−1		y0+3
−		=
	y0−1		x0+1

−(x₀−1)(x₀+1)=(y₀+3)(y₀−1) (x₀−1)²+(y₀−1)²=4 (x₀²−1)+(y₀²+2y₀−3)=0 x₀²−2x₀+1+y₀²−2y₀+1−4=0 x₀²+y₀²+2y₀−4=0 x₀²−2x₀+y₀²−2y₀−2=0 x₀²−x₀²+y₀²−y₀²+2y₀−(−2y₀)+0−(−2x₀)−4−(−2)=0 2x₀+4y₀−2=0 x₀=1−2y₀ x₀=1−2y₀ (1−2y₀)²−1+y₀²+2y₀−3=0 x₀=1−2y₀ 1−4y₀+4y₀²−1+y₀²+2y₀−3=0 x₀=1−2y₀ 5y₀²−2y₀−3=0

	2+8
y0=		=1
	10

	2−8		3
y0=		=−
	10		5

Punkty styczności to (−1,1)

	11		−3
(		,		)
	5		5

	6	(5)
y=−			(x+1)−3
	5	(−8)

x=−1

	3		9
y=		x−
	4		4

x=−1 Skorzystałem z pochodnej funkcji uwikłanej, dwupunktowego równania prostej współczynnik kierunkowy to tangens kąta nachylenia prostej do osi OX z tego że styczna musi mieć punkt wspólny z krzywą

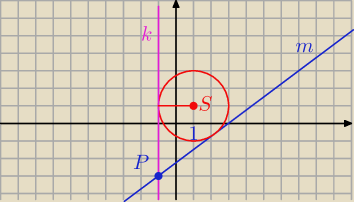
Janek191: (x −1)² + ( y − 1)² = 4'wiec S = (1, 1) r = 2 Prosta styczna do okręgu y = a x + b ma przechodzić przez punkt P = (−1, −3) czyli − 3 = − a + b ⇒ b = a − 3 Prosta styczna ma równanie y = a x + a − 3 lub a x − y + a − 3 = 0 Odległość tej prostej od środka okręgu S = ( 1, 1) jest równa r = 2 więc

I a*1 − 1*1 + a − 3 I
	= 2
√a2 + 1

I 2a − 4 I = 2 √a² + 1 ( 2 a − 4)² = 4*( a² + 1) 4 a² − 16 a + 16 = 4 a² + 4 16 a = 12

	3
a =
	4

	3		3		9
y =		x + U{3}[4} − 3 =		x −
	4		4		4

	3		9
Odp. m : y =		x −
	4		4

====================== k : x = − 1 − równanie II stycznej.