trygonometria zuza: wykaż, że jeśli a²=H*h, to sinα=√2−1

6latek: Wykazalas

zuza: nie

zuza: ups.. nie napisałam głównej treści zadania W trójkącie równoramiennym długość podstawy wynosi a, wysokość opuszczona na podstawę i ramię są równe odpowiednio H i h. Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę α. I teraz wykaż ....

zuza: up

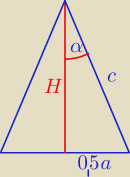
Janek191: Mamy a² = H*h oraz 0,5 a*H = 0,5 c*h / * 2 ⇒ a*H = c*h Dzielimy stronami

a2		H*h
	=
a*H		c*h

	a		H		H2
		=		⇒ a =
	H		c		c

	0,5 a		a		H2   c		H2		H
sin α =		=		=		=		= 0,5*(		)2
	c		2c		2 c		2 c2		c

sin α = 0, 5 cos²α sin α = 0,5*( 1 − sin² α) 0,5 sin² α + sin α −0,5 = 0 sin²α + 2 sin α − 1 = 0 Δ = 4 − 4*1*(−1) = 8 = 4*2 √Δ = 2√2 więc

	− 2 + 2√2
sin α =		= √2 − 1
	2

=========================

g: Pole S = H*h*sinα = a²*sinα = 1/2 a*H

	H		1		cosα
sinα =		=		=
	2a		4 tgα		4 sinα

4 sin²α = cosα = √1−sin²α 16 sin⁴α + sin²α − 1 = 0 Δ = 65

	−1 +√65
sin2α =		inny wynik
	32

Janek191: Skąd te wzory w I wierszu ?

g: Z treści wynikało że h to jest ramię, czyli c na rysunku.

Janek191: h − wysokość do ramienia c

Janek191: Taki rysunek jak u mnie

g: W takim razie ja rozwiązałem inne zadanie.

zuza: Dzięki Janek191

Janek191: Wszystko zrozumiałe ?

zuza: Tak, tak, zrozumiałe. Tylko jak wpaść na taki pomysł Mam jeszcze jeden dowód, jeśli możesz pomóc: Wykaż że jeżeli długości boków trójkąta ABC spełniają warunek IABI² = IBCI*IACI+IACI², to kąt przy wierzchołku C ma miarę dwa razy większą niż kąt przy wierzchołku B.