1. Cysterna kolejowa do przewodu chemikaliów składa się z trzech części: części środkowej w
kształcie walca oraz dwóch części w kształcie półkul, zamykających z obu stron część środkową.
Część walcową cysterny wykonuje się z pojedynczej warstwy blachy, a części półkuliste z warstw
podwójnych. Objętość cysterny ma być równa 18pi m3.
a) zbadaj, jaka powinna być średnica i długość cysterny, aby na jej wykonanie zużyć jak
najmniej materiału.
b) wiadomo, że 1m2 blachy kosztuje 500 zł. Oblicz, ile wynosi koszt materiału potrzebnego do
wykonania tej cysterny.
2. Należy wykonać ze szkła otwarte naczynie w kształcie walca o pojemności pi dm3 i grubości
ścianek oraz dna równej 2 cm. Przekrój osiowy naczynia pokazany jest na rysunku.
a) Zbadaj, jaka powinny być wewnętrzne wymiary tego naczynia, aby jego masa była możliwie
najmniejsza.
b) Gęstość szkła jest równa 2500 kg/m3. Oblicz masę tego naczynia.
Jak ruszyć te zadania? W 1. mam wrażenie, że brakuje jakiejś danej, a w drugim nie wiem, jak
znaleźć promień lub wysokość (bądź od czego uzależnić).
Zadania pochodzą ze zbioru zadań Andrzeja Kiełbasy.
Do 2 zaraz dodam rysunek.
to, co na zielono, ma 2 cm
krzywo przerywana kreska wyszła, powinna być bardziej na środku
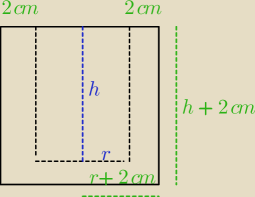zad.2
P − pojemność naczynia
P = π dm3 = 1000π cm3
P= π*r2*h r>0, h>0
| 1000 | ||
π*r2*h = 1000π r2*h = 1000 h = | ||
| r2 |
| 1000 | ||
Vs = π*(r+2)2*(h+2) −1000π = π*(r+2)2*( | +2) −1000π | |
| r2 |
| 1000 | ||
f(r) = π*(r+2)2*( | +2) −1000π | |
| r2 |
| 4 | ||
V = πr2*H + | πf2 | |
| 3 |