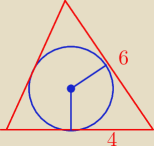
Kula wpisana w stożek Kazimierz: Oblicz promień kuli wpisanej w stożek o promieniu podstawy 4 i tworzącej równej 6. Tak więc obliczyłem sobie wysokość trójkąta, który jest przekrojem osiowym tego stożka. H = 8√5 Następnie policzyłem pole trójkąta, które wynosi 32√5 Promień kuli, czyli także okręgu wpisanego w ten trójkąt wyznaczyłem za pomocą wzoru na pole trójkąta: P = ((a + b + c) * r) / 2 Porównałem oba pola i wyszło mi r = 16√5 / 5 W odpowiedziach jest podany wynik r = 4√5 / 5 Mam do was pytanie. Czy w odpowiedziach jest błąd, czy ja go gdzieś popełniłem ?

Janek191: h² + 16 = 36 h = √20 = 2√5 P = 0,5*8*2√5 = 8√5 L = 20

	16√5		4√5
r =		=
	20		5

Janek191:

	2 P
r =
	L

Kazimierz: Okej, coś mi się poplątało i pod wysokość podstawiłem wartość P = 8√5. Dzięki za pomoc.