STYCZNA DO WYKRESU FUNKCJI EMPE: W którym punkcie należy przyłożyć styczną do wykresu funkcji f(x) = −x³, aby styczna ta

	32
odcinała z pierwszej ćwiartki układu współrzędnych trójkąt o polu		?
	3

Z góry dziękuję za pomoc!

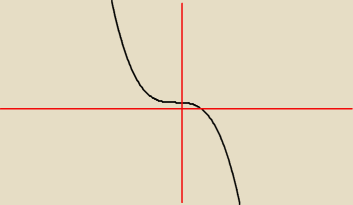
olekturbo: f(x) = −x³ f'(x) = −3x² f'(2) = −12 f(2) = −8 y = −12x+b −8 = −24+b b = 16 y = −12x+16 y = 16

	4
x =
	3

spr.

	1		4		32
P =		*		* 16 =
	2		3		3

EMPE: Odpowiedź jest, że w punkcie (2; −8)

EMPE: W sumie to Ci wychodzi, ale jak wpadłeś na pomysł, żeby liczyć wartość funkcji i pochodnej dla 2?

olekturbo: Liczylem najpierw dla jedynki, nie wyszlo, to policzylem dla dwojki

EMPE: No i dobrze Ci wyszło, ale to tak jakbyś strzelał. Myślałem, że jest jakaś metoda na znalezienie x_o.