planimetria: twierdzenie sinusów mia: W trójkąt T o kątach: α, β, π−α−β wpisano okrąg O o promieniu r. Wyznacz pole trójkąta, którego wierzchołkami są punkty styczności trójkąta T i okręgu O.

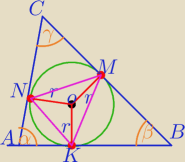
Mila: γ=180^o−(α+β) ∡KOM=180−β ∡KON=180−α ∡NOM=180−(180^o−(α+β))=α+β

	1
PΔNMK=		*[r2*sin(180−α)+r2*sin(180−β)+r2*sin(α+β)]=
	2

r2*(sinα+sinβ+sin(α+β))
2