ostroslup
fiz666:
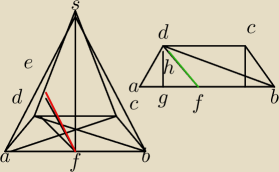
odstawą ostrosłupa ABCDS jest trapez ABCD . Przekątna AC tego trapezu ma długość 8
√3 , jest
prostopadła do ramienia BC i tworzy z dłuższą podstawą AB tego trapezu kąt o mierze 30∘ .
Każda krawędź boczna tego ostrosłupa ma tę samą długość 4
√5 . Oblicz odległość spodka
wysokości tego ostrosłupa od jego krawędzi bocznej SD .
Ja to widzę tak:
trójkąt ABC jest prostokątny, wszystkie krawędzie ostrosłupa sa równe, więc spodek leży w
połowie przeciwprostokątnej
plan jest taki:
1) obliczyć przekątną DB i ramię trapezu
2) obliczyć wysokość FS z tw. Pitagorasa
3) porównać wysokości w trójkącie dfs. Tylko skąd wziąć ten odcinek DF?
