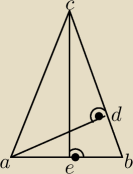
Oblicz cosinusy wszystkich kątów wewnętrznych trójkąta ABC Sawyer: W trójkącie równoramiennym ABC , w którym |AC| = |CB| Wysokość |CE| jest dwa razy dłuższa od wysokości AD (patrz rysunek). Oblicz cosinusy wszystkich kątów wewnętrznych trójkąta ABC . Z góry dziękuje.

Janek191: Mamy P_Δ = 0,5 I AB I*I CE I = 0,5 I BC I * I AD I ⇒ I AB I * I 2 AD I = I BC I * I AD I ⇒ 2 I AB I = I BC I

	I EB I		0,5 I AB I		0,5 IAB I
cos β =		=		=		= 0,25
	I BC I		I BC I		2 I AB I

cos α = cos β = 0,25 oraz I CE I² + I 0,5 AB I² = I BC I²

	1		15
I CE I2 = I BC I2 − I 0,25 BC I2 = I BC I2 −		I BC I2 =		I BC I2
	16		16

	√15
I CE I =		I BC I
	4

więc

	I CE I		√15
cos δ =		=
	I BC I		4

	15		14		7
cos γ = cos (2δ) = 2 cos2δ − 1 = 2*		− 1 =		=
	16		16		8

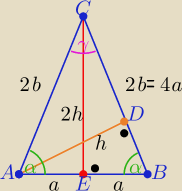
Eta: |AB|=2a , |AC|=|BC|=2b P(ABC)= a*2h i P(ABC)= b*h ⇒ b=2a

	a		1
z trójkąta prostokątnego EBC :cosα=		=
	4a		4

z twierdzenia kosinusów w trójkącie ABC:

	16a2+16a2−4a2		7
cosγ=		=
	2*4a*4a		8

i po ptokach

Janek191: Tomek nie jest zainteresowany rozwiązaniem

Eta: "rozwlekłym" rozwiązaniem

Janek191: Lepiej takie, niż żadne

Kacper: Eta nie ładnie

Jack:

Eta:

Janek191: Eta lubi mi dokuczać

Eta: Co? nie podoba Ci się Kacper : krótkie rozwiązanie?

Eta: Dokładnie ... Janek

Kacper: Właśnie to dokuczanie Eta

Eta: Mogę opuścić forum