Dla jakich wartości parametru k równanie ma dwa rozwiązania przeciwnych znaków Sawyer: Dla jakich wartości parametru k równanie x²−|2x − 3| = k³ + 5 ma dwa rozwiązania przeciwnych znaków? Wiem że x1*x2<0 co oznacza że ^c_a<0 z czego a = 1. wartość bezwzględna zmienia swój znak w ³₂. Czyli dla pierwszego przypadku od (−∞; ³₂) jest ujemna: x² + 2x − 3 − k³ − 5 = 0 x² + 2x − k³ − 8 = 0 c = −k³ − 8 c < 0 −k³ < 8 k > −2 dla drugiego przypadku od(³₂; +∞) jest dodatnia: x² −2x + 3 − k³ − 5 = 0 x² − 2x − k³ − 2 = 0 c = −k³ − 2 c < 0 −k³ < 2 k³ > −2 k > −³√2 Problem jest taki, że nijak nie zgadza mi się to z wykresem funkcji. I jakoby z niego wynika że drugie rozwiązania dla k (czyli to k > −³√2) muszę odrzucić. I nie mam pojęcia dlaczego. Z góry dziękuje za pomoc.

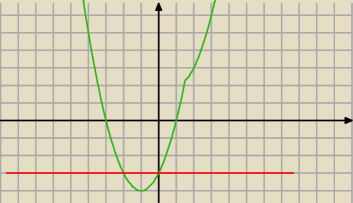
Jerzy: czerwona: y = k³ + 5

Godzio: Nie bierzesz pod uwagę, że pierwiastki znajdują się w odpowiednich przedziałach. Lepiej robić z wykresem, jeśli chcesz będę mógł Ci to rozpisać

Sawyer: Jerzy: Nie do końca rozumiem Twoje uzasadnienie. Mógłbyś wyjaśnić jak chłopu na roli ? Godzio: A mógłbyś to rozwiązać algebraicznie? Ponieważ nie wiem czemu miałbym w ogóle ustalać jakikolwiek przedział dla wartości K.

Sawyer: Jerzy: Znaczy widzę że od tej linii w "górę" rozwiązania będą innych znaków. Ale jak mam znaleźć jej równanie.

Jerzy: Zauważ,że jesli tylko podniesieś czerwoną linię do góry, to przetnie zieloną w punktach o odcietych przeciwnych znaków

Jerzy: obecnie: k³ + 5 = −3 ( widać na wykresie ) , a jak podniesiesz do góry, to ?

PrzyszlyMakler: Ale skąd znalazłes równanie tej prostej?

Jerzy: Podane jest w treści zadania ( prawa strona równania )

Jerzy: A jeśli pytasz dlaczego : y = − 3 ... podstaw z lewej strony: x = 0

Sawyer: Jerzy: K³>−8 ? No ale powiedzmy że nie mam takiego luksusu jak rysowanie wykresu i chciałbym znaleźć równanie tej prostej algebraicznie. Jak dojść do tego że k³ + 5 = −3 i że w takim układzie k³ > 8 (czyli w góre od niej) przecina równanie w rozwiązaniach o odmiennych znakach

Sawyer: Jerzy: no dobra rozumiem. A czemu moje podejście do zadania jest złe?

Jerzy: Algebraicznie.... rozbijasz na dwa równania kwadratowe ( w przedziałach) i dobierasz takie warunki ( dla parametru k), aby trójmian miał dwa pierwiastki różnych znaków: Δ>0 x₁*x₂ < 0 x₁ + x₂ < 0

Godzio:

	3
Zajmę się najpierw przedziałem x ∊ (−∞,		>
	2

	3
Jeden pierwiastek musi znajdować się w przedziale (−∞,0), a drugi (0,		>.
	2

Mamy funkcję f(x) = x² + 2x − k³ − 8 Δ > 0 f(0) < 0

	3
f(		) ≥ 0
	2

− skąd te warunki? Narysuj parabolę spełniającą warunki zadania (dowolną), i zobacz co musi być spełnione, aby to zaszło Δ = 4 + 4k³ + 32 = 4k³ + 36 > 0 ⇒ k³ > −9 ⇒ k > −³√9 ≈ −2,08 f(0) = − k³ − 8 < 0 ⇒ k³ > − 8 ⇒ k > −2

	3		9		11		11
f(		) =		+ 3 − k3 − 8 = −		− k3 ≥ 0 ⇒ k3 ≤ −
	2		4		4		4

	3√11
stąd k ≤ −		≈ − 1,4
	3√4

	3√11
k ∊ (−2,−		>
	3√4

	3
Teraz dla zajmijmy się przypadkiem, gdy mamy jedno rozwiązanie ujemne dla x ∊ (−∞,		>
	2

	3
oraz jedno rozwiązanie dodatnie dla x ∊ (		,∞) oraz
	2

	3
W pierwszym przypadku interesuje nas przypadek gdy x1 < 0 oraz x2 >		.
	2

Wówczas równanie posiada tylko jedno rozwiązanie bo x₂ nie należy do rozpatrywanego przypadku: Δ > 0 ⇒ k > −³√9 f(0) < 0 ⇒ k > −2

	3		3√11
f(		) < 0 ⇒ k > −
	2		3√4

	3√11
Cześć wspólna to k > −
	3√4

Teraz bierzemy funkcję dla drugiego przedziału:

	3
f(x) = x2 − 2x − k3 − 2 i warunki na jeden pierwiastek w przedziale (		,∞)
	2

Δ > 0 ⇒ 4 + 4k³ + 8 = 4k³ + 12 > 0 ⇒ k > −³√3

	3		9		11		3√11
f(		) < 0 ⇒		− 3 − k3 − 2 = −		− k3 < 0 ⇒ k > −
	2		4		4		3√4

	3√11
Biorąc część wspólną mamy: k > −
	3√4

	3
Teraz bierzemy część wspólną z warunkami z przedziału (−∞,		> i mamy:
	2

	3√11
k > −
	3√4

Ostatecznie sumujemy przedziały z dwóch przypadków i mamy:

	3√11		3√11
k > −		lub k ∊ (−2,−		>
	3√4		3√4

Co ostatecznie daje odpowiedź: k > −2 Jak widać wyliczenia nie są łatwe i trzeba przejść kilka etapów

Jerzy: A czy jest zakaz wspomagania się szkicem wykresu ?

Godzio: Teoretycznie trzeba by było jeszcze liczyć przypadek gdy

	3		3
Δ = 0 i x0 < 0 gdy x ≤		oraz Δ = 0 i x0 > 0 gdy x >
	2		2

Sawyer: Jerzy: Ok, rozumiem. I dziękuje. Jednak jestem debilem. Po pierwsze: Rozwiązanie z tym równaniem prostej które podałeś jest o niebo łatwiejsze. A po drugie: Jeśli mam k > −2 a w drugim przypadku k > −³√2 to drugi przypadek jest podzbiorem pierwszego i biorę sumę czyli po prostu zbiór pierwszy => k>−2. Godzio: Również dziękuje. Ok, uznajmy że temat zamknięty. Chyba że dalej jakoś źle myślę.

Godzio: Sawyer, powtórzę. Nie możesz po prostu liczyć dla przypadków parametr k. Rozpisałem Ci, że w danym przypadku może się zdarzyć, że masz dwa rozwiązania − jedno ujemne drugie dodatnie. No

	3
to weźmy przypadek gdy x ∊ (−∞,		), nakładasz warunek, że x1x2 < 0, ale co gdy x1 =
	2

−5, a x₂ = 4, przecież 4 nie należy do tego przedziału, więc tak jakby nie istnieje to rozwiązanie. Rozumiesz?

Sawyer: Godzio: No właśnie analizuje Twoje obliczenia. I oczywiście masz rację. Widzę że to zadziałało po prostu dla tego równania, racja. Muszę brać pod uwagę w ogóle istnienie miejsca zerowego − a ja założyłem bezpodstawnie że istnieje w takim przedziale. Będę pamiętał.