2
Zaq: oblicz pole
∫∫ e
−x2−y2dxdy
d
d: x
2+y
2≤a
2
wychodzi mi wynik
mógłby ktoś sprawdzić ?
4 maj 18:40
Jerzy:
Pokaż granice całkowania i całkę z jakobianem
4 maj 18:48
Jerzy:
Napisałem Ci w innym poście....zła całka
4 maj 18:51
Zaq: zapomniałem o jakobianie
czyli:
2π a
∫ dα ∫ e−r2r dr
0 0
tam w potędze e skróciło się z jedynki trygonometrycznej.
czy tak będzie ?
4 maj 18:54
Jerzy:
Dobrze...tylko dopisz różniczkę dα
4 maj 18:56
Zaq: tylko teraz nie wiem jak się zabrać za całkę
∫re−r2 dr
4 maj 19:01
Zaq: przez części może ?
4 maj 19:04
Jerzy:
Nie..podstaw: −r2 = t
4 maj 19:07
4 maj 19:13
Zaq: ostatecznie wyszło mi
π(e−a2−1)
4 maj 19:16
Jerzy:
Całka dobra...pokaż dalsze obliczenia
4 maj 19:24
Zaq: dalej liczę oznaczoną od 0 do a
wychodzi:
potem liczę z tego całkę nieoznaczoną po dα
i tu nie jestem pewny
dalej oznaczona z tego od 0 do 2π
no i wynik tak jak wcześniej napisałem
4 maj 19:37
Zaq: jak to wygląda ?
4 maj 19:56
Jerzy:
= πe−a2
4 maj 20:06
Zaq: a jak podstawie pod −12e−r2
zero to nie wyjdzie 12?
4 maj 20:11
Jerzy:
Zaraz .... ja się pomyliłem ... liczę
4 maj 20:12
Jerzy:
Masz dobrze
4 maj 20:13
Zaq: Dziękuję bardzo za pomoc,
Mam jeszcze zadanie oblicz objętość bryły ograniczonej powierzchnią
x+y+z+=1
i pł. układu wsp
Jak to będzie wyglądało na rysunku ?
4 maj 20:17
Jerzy:
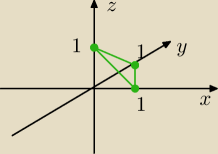
4 maj 20:23
Zaq: mam jeszcze problem z minusem w tym pierwszym zadaniu.
przed podstawieniem granicy od 0 do a było
a po podatawieniu zostało
4 maj 22:10
Jerzy:
| 1 | | 1 | | 1 | |
| e−(0)2 = |
| *1 = − |
| |
| 2 | | 2 | | 2 | |
4 maj 22:13
Jerzy:
| | 1 | |
a.... racja, ma być + |
| |
| | 2 | |
4 maj 22:14
jc: ∫∫ = π (1 − e−a2)
4 maj 22:19
4 maj 22:21
4 maj 22:25
Zaq: dobra mam taki wynik jak napisał jc, dziękuję
4 maj 22:26
