geometria Kamil18: Planimetria na mature W trójkącie ABC bok BC jest najdłuższy. Punkty M i N leżą w trójkącie. Wykaż że MN<BC. Może ktoś pokazać dowód tego?

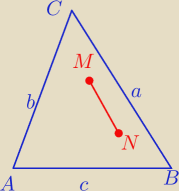
Janek191: 1) Przypadek.

Kamil18: No to akurat wiem ze bedzie zawsze krótrszy. Szczególnie jak bedzie równoległy. ale intersuja mnie inne przypadki. I jak dowieść tego dla dowolnych dwóch punktów N,M w trójkącie ABC

Kamil18: Czy może ktoś podać dowód tego?

wmboczek: AM<CM AN<AB ∡MAN≤∡CAB z tw cosinusów mamy zatem ...

Kamil18: Czemu AM<CM?

Kamil18: Czy ktoś to umie?

Kamil18: ?

Kamil18: Mozna to zrobic tak: Niech MN przecia boki trójkata w punktach D i E, więc DE jest krótszy niż trzeci bok. Stąd tak ze jest mniejszy od BC. Czy to jest dobrze? Bo nie wiem jak uzyć tw cosinusów co napisał wmboczek