bryła obrotowa - romb klp: Romb o boku długości a obraca się dokoła jednej z przekątnych. Wyznacz pole tego spośród takich rombów, dla którego objętość otrzymanej bryły jest największa. Otrzymana bryła to dwa złączone (podstawami) stożki, więc jej objętość to V=2/3πr²h Wiem jak rozwiązuje się tego typu zadania, ale mam problem z wyrażeniem przekątnej, czyli wysokości lub promienia bryły, za pomocą danego boku "a".

===: Przekątne rombu przecinają się pod kątem prostym i dzielą się na połowy. Stary ... poczciwy "PieciaGoras" na pewno Ci pomoże

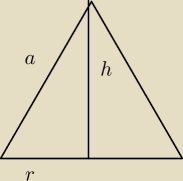
klp: czyli jak mam połowę rombu jak na rysunku, czyli przekrój połowy otrzymanej bryły, to zapisuje r²=a²−h² i rozwiązuje dalej równanie podstawiając do wzoru, licząc pochodną itp. przy czym h traktuje jako parametr ?

Tadeusz: a to Ty masz dane Wyznacz r poprzez h

klp: Właśnie jedyna dana jaką mam to to, że bok rombu wynosi a, więc mam lekką zagwozdkę co dalej robić. Spróbowałem zrobić tak jak napisałem wyżej i pochodna wyszłą V(a)=2π/3*a²*h−h³, ale pochodna z tego to funkcja liniowa z minimum, czyli nie policzę z tego największej objętości bryły...