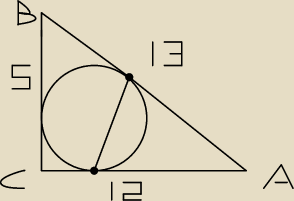
 W trójkąt prostokątny ABC o przyprostokątnych długości |BC | = 5 i |AC | = 12 wpisano okrąg.
Oblicz długość odcinka łączącego punkty wspólne okręgu wpisanego z bokami AB i AC.
Nie mam specjalnie pomysłu na to zadanie. Jakieś podobieństwa trójkątów może? Dobrze wykonałem
chociaż rysunek? Nie musicie rozwiązywać całego zadania, ale chociaż naprowadźcie mnie na
rozwiązanie.
W trójkąt prostokątny ABC o przyprostokątnych długości |BC | = 5 i |AC | = 12 wpisano okrąg.
Oblicz długość odcinka łączącego punkty wspólne okręgu wpisanego z bokami AB i AC.
Nie mam specjalnie pomysłu na to zadanie. Jakieś podobieństwa trójkątów może? Dobrze wykonałem
chociaż rysunek? Nie musicie rozwiązywać całego zadania, ale chociaż naprowadźcie mnie na
rozwiązanie.
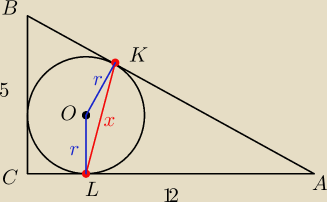 kąt LOK=α oraz kąt CAB=180−α
x2=r2+r2−2r2cos(180−α)=2r2+2r2sinα=2r2(1+sin(180−α))
kąt LOK=α oraz kąt CAB=180−α
x2=r2+r2−2r2cos(180−α)=2r2+2r2sinα=2r2(1+sin(180−α))
| BC | ||
sin(180−α)=sinα= | ||
| AB |
| 2P | ||
r= | ||
| AB+BC+AC |
| 12+5−13 | ||
r= | =2 | |
| 2 |
| 12 | ||
cosα= | ||
| 13 |
| 12 | ||
x2=10+10−2*10*10* | ⇒ x= ............. | |
| 13 |
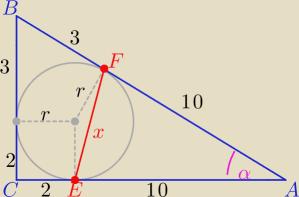
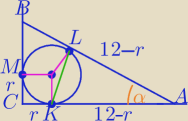 Np. tak:
1)
oblicz pole ΔABC
2) oblicz r z wzoru P=p*r
Np. tak:
1)
oblicz pole ΔABC
2) oblicz r z wzoru P=p*r
| 12 | ||
3)cosα= | ||
| 13 |
| 12 | ||
x2=102+102−2*10*10* | ||
| 13 |

 ojoj... ale namieszałem :c
cos(180−α)=−cosα
przepraszam, za dużo statystyki nieogarniętej
ojoj... ale namieszałem :c
cos(180−α)=−cosα
przepraszam, za dużo statystyki nieogarniętej