mat hegel: dla jakich wartości parametru a układ równań x²+y²=a (x+y)²=36 będzie miał 2 rozwiązania

Metis: (x+y)²=6² x+y=6 y=6−x x²+(6−x)²=a x²+x²−12x+36=a 2x²−12x+36−a=0 Δ=0 ⇔ 144−4*2*(36−a)=0 144−8(36−a)=0 ⇔ a=18 I to jest poprawna odpowiedź.

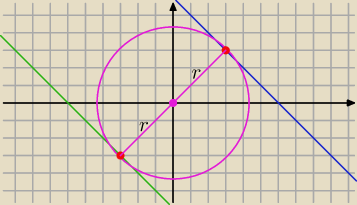
Eta: (x+y)²−36=0 ⇒ (x+y−6)(x+y+6)=0 ⇒ x+y−6=0 v x+y+6=0 −−− dwie proste równoległe x²+y²=a −− okrąg o środku S(0,0) i r=√a , a>0 układ ma dwa rozwiązania jeżeli odległość d między prostymi będzie równa 2r =2√a czyli proste muszą być styczne do okręgu

	|6+6|		12
d=		=
	√2		√2

to 12=2√2a ⇒ √2a=6 ⇒ 2a=36 ⇒ a=18

Eta: @Metis (x+y)²=36 ⇒ x+y=6 lub x+y= −6