planimetria Eta: Zadania z planimetrii tylko dla maturzystów Zad1/ wykaż,że jeżeli w trójkącie o kątach α, β, γ zachodzi równość sinα=2sinβcosγ to trójkąt jest równoramienny zad2/ Wykaż,że ,okrąg wpisany w trójkąt prostokątny jest styczny do przeciwprostokątnej w punkcie dzielącym ją na dwa odcinki, których iloczyn długości jest równy polu tego trójkąta zad3/ W trójkąt ABC wpisano romb tak,że wspólnym kątem jest kąt BAC. Stosunek boków trójkąta zawierających ten kąt jest równy m Wyznacz stosunek pola rombu do pla tego trójkąta zad4/ W trójkącie ABC na bokach AB i AC wybrano odpowiednio punkty M i N tak,że |AM|: |MB|=1:2 oraz |AN|: |NC|=2:1 Wykaż,że stosunek |NK|: |KB|=1:6 , gdzie K jest punktem przecięcia odcinków CM i BN Powodzenia

Ajtek: O, to dla mnie w sam raz . Witaj Eta

Eta: Łap.............. tylko

PrzyszlyMakler: Czy w zadaniu 1 mogę rozpocząć udowadnianie od "jeżeli trójkąt co jest równoramienny" i oznaczyć go równoramiennie?

Eta: Możesz, ale koniecznie z komentarzem: "Załóżmy,że taki trójkąt jest równoramienny" to............

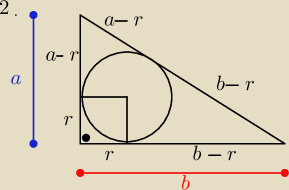Jack: wykazac, ze (a−r)(b−r) = Pole trojkata. (a−r)(b−r) = ab − ar − br + r² = ab − r(a+b) + r² z Pitagorasa : a²+b² = (a+b−2r)² a²+b² = a²+2ab+b² − 4r(a+b) + 4r² 2ab − 4[r(a+b) − r²] = 0 // : 2 ab − 2[r(a+b) − r²] = 0 ⇔ ab = 2[r(a+b) − r²] (a−r)(b−r) = 2[r(a+b) − r²] − r(a+b) + r² = 2r(a+b) − 2r² − r(a+b) + r² = r(a+b) − r²

	1		1
P =		* a * b =		* 2[r(a+b) − r2] = r(a+b) − r2
	2		2

c.n.w.

Eta: Jest krótszy sposób

Jack: mozna na pewno latwiej oznaczyc... ale ja robilem po swojemu ; x

Eta:

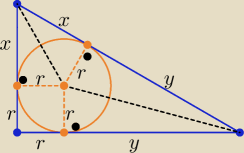Eta: P=r²+xr+yr 2P=(x+r)(y+r)= xy+xr+yr+r² ⇒ 2P=xy+P ⇒ P=xy c.n.w

takamyśl: No tak P=pr To się nazywa ładne rozwiązanie

Krzysiek: Eta, czemu P = r² + xr + yr ?

Jack: @Krzysiek

	1		1
Pole =		r * obwód =		r (2x+2y+2r) = r(x+y+r) = ...
	2		2

Paweł: Dobry wieczór wszystkim, chodzi o zadanie nr 1, czy jeśli doszedlem do postaci sin( γ − β) = 0 to to wykazuje, że mamy do czynienia z trójkątem równoramiennym?

Saizou : jeszcze rozwiąż równość sin(γ−β)=0 <=> γ=β (bo suma miar kątów w trójkącie wynosi 180)

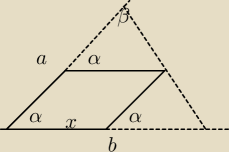Damian: ^a_b=m z podobienstwa ^a_b=^a−x_x=m ^a_x=m+1 P_rombu=2 * 1/2*x*x*sinα i x = ^a_m+1 P_trojkata= 1/2*a*b*sinα i b= ^a_m ^{P rombu}_{P trojkata}=^2m_(m+1)²

Eta:

Eta: Damian ( tylko czy na pewno jesteś maturzystą?

Paweł: Dzięki Saizou

Krzysiek: Ja nie jestem maturzystą

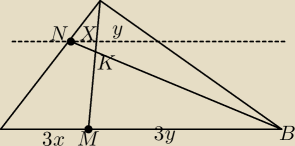Damian: niestety jestem, chciałbym mieć to za sobą 4. przerywana jest równoległa do podsawy korzystam z treści 2 * 3x= 3y y=2x wiec 3y = 6x ΔNKX podobny do ΔBKM wiec 6* |NK|= |BK|

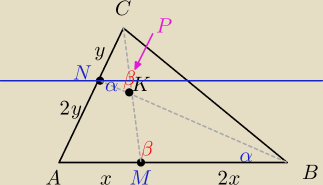Jack: zad4/ W trójkącie ABC na bokach AB i AC wybrano odpowiednio punkty M i N tak,że |AM|: |MB|=1:2 oraz |AN|: |NC|=2:1 Wykaż,że stosunek |NK|: |KB|=1:6 , gdzie K jest punktem przecięcia odcinków CM i BN. ............................................................................ ............................................................................ ............................................................................ z podobienstwa CNP i CAM (kkk)

y		3y
	=
|NP|		x

x = 3|NP| z podobienstwa NKP i KMB (kkk)

|NK|		|NP|
	=
|KB|		2x

	x
skoro x= 3|NP| to |NP| =
	3

zatem

|NK|		x   3		x		1
	=		=		=
|KB|		2x		6x		6

c.n.w.

Jack: aaa...ktos to juz rozwiazal... : (

Eta: Komentarz nieco za ubogi 1/ rysuję odcinek równoległy do podstawy i przechodzący przez punkt N 2/ trójkąty podobne ... z jakiej cechy ? należy zaznaczyć na rys. odpowiednie kąty 3/ tezę napisać w postaci |NK|: |KB|=1:6 4/ c.n.w

Eta: dla Jacusia za wyczerpujący dowód

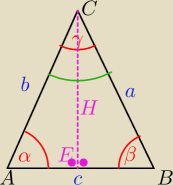Metis: 1) Załóżmy,że taki trójkąt jest równoramienny. Musimy zatem wykazać, że równanie sinα=2sinβcosγ jest prawdziwe. Przejdźmy do dowodu. Niech A,B,C będą kolejnymi wierzchołkami trójkąta równoramiennego ABC , a kąty α, β,γ przyległe kolejno do podanych wierzchołków. |AB| =c − podstawa rozpatrywanego trójkąta |BC|=a, |AC|=b − ramiona ... |AC|=|BC| ⇔a=b Prowadzimy odcinek |CE| będący wysokością i dwusieczną kąta ACB, stąd:

	1		γ
|CE|=H i ∡BCE=∡ACE=		∡ACB=
	2		2

Wykażemy, że P=2sinβcosγ=sinα=L Z trójkąta EBC:

	|CE|		H
sinβ=		⇔ sinβ=
	|CB|		a

Z twierdzenia cosinusów w ABC: |AB|²=|BC|²+|AC|²−2*|AC|*|BC|*cosγ ⇔ −|AB|²=−|BC|²−|AC|²+2*|AC|*|BC|*cosγ ⇔ −c²=−a²−b²+2*b*a*cosγ

	−c2+a2+b2
cosγ =
	2ab

	−c2+2a2
cosγ=
	2a2

Wyrażamy |AB|=c za pomocą odcinka |CE|=H: Z trójkąta prostokątnego CEB:

	1
|CE|2+|EB|2=|CB|2 ⇔ H2+		c2=a2 , stąd
	4

1
	c2=a2−H2 /*4
4

c²=4(a²−H²) , stąd:

	−4(a2−H2)+2a2
cosγ=
	2a2

Coś źle

	CE		CE		H
sinα=		=		=
	AC		CB		a

Eta: zad5/ W prostokącie stosunek boków |AB|: |AD|=√2 Punkt M jest środkiem boku AB. Wyznacz miarę kąta między AC i MD

pablito: Czy mógłby ktoś troszke pierwsze rozpisac ?

Metis: Etuś czy tam muszę H wyrazić za pomocą ramion?

Paweł: α + β + γ = 180 Wyznacz sobie któryś jeden kąt i potem ze wzorów z tablic w trygonometrii.

Eta: zad6 W trapezie miary katów przy krótszej podstawie wynoszą 120^o i 150^o Różnica kwadratów przekątnych tego trapezu wynosi 20 Oblicz pole trapezu

Metis:

Eta: Metisku Znajdź prostsze rozwiązania ( bo czasu na maturze Ci zabraknie wskazówka α+β+γ=180^o ⇒ α= 180^o−(β+γ) ..........

Metis: Stres już mnie zżera

Paweł: Największy wróg maturzysty po lenistwie

olekturbo: Eta, znałazlem przekątne √10 i √30. Co teraz? (6)

Mila: Metis: ad (1) sinα=sin(180−(β+γ))=sin(β+γ) sinα=sin(β+γ) lewa z założenia, prawa z wzoru i może coś wyjdzie?

maturalna: w zad 6 przyda sie (a+b)(a−b)=20 i obliczenie a−b z zaleznosci miedzy katami

maturalna: i z wysokosci poprowadzonych z wierzchołków katów rozwartych

Metis: Dziękuje Milu , ale to już może ktoś inny dokończy. Jutro pracowity dzień.

olekturbo: Eta ad.6 5√3 ?

Eta:

olekturbo:

Paweł: A zad.5 ktoś ruszał?

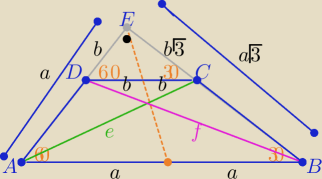Eta: f²=b²+3a² e²=a²+3b² − −−−−−−−−−−−−−−−− f²−e²=2a²−2b² ⇒ a²−b²=10

	a2√3		b2√3		√3		√3
P(trapezu)= P(ABE)−P(DCE) =		−		=(a2−b2)*		=10*		=
	2		2		2		2

= 5√3 [j²]

Mila: Dobranoc

Eta: Miłych snów

Eta: Zostało jeszcze zad.5/

Metis: Na wynos

Eta:

Eta: zad5/ wciąż czeka na ................

Metis: Próbowałem z podobieństwa i pola ale nic z tego

Eta: Myśl dalej (nie jest trudne Wieczorem ( jak nikt z maturzystów nie rozwiąże) podam rozwiązanie

Metis: Policzyłem też przekątną Ale nie wiem w jakim stosunku punkt przecięcia tych odcinków dzieli te odcinki.

Eta: Jeden ze sposobów ( ale jest łatwiejszy Możesz użyć "narzędzi" geometrii analitycznej ( odpowiednio umieszczając prostokąt w układzie współrzędnych) i znajdując miarę kąta między prostymi Próbuj ( aż do sukcesu)..........

Kacper: Zadanie 5 jest fajne Można podać przynajmniej... 4 sposoby rozwiązania

takamyśl: W zad 5. Możliwe, że wychodzi 90^o?

Eta: Dokładnie ...kąt prosty

takamyśl: Uff Troszkę rozpisania i twierdzenie cosinusów.

Kacper: Wystarczy twierdzenie Pitagorasa Czyli mamy 6 sposób

Metis: Dwa razy Pitagoras pewnie

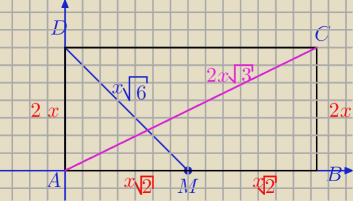Jack: zad 5./ W prostokącie stosunek boków |AB|: |AD|=√2 Punkt M jest środkiem boku AB. Wyznacz miarę kąta między AC i MD na szybko bo czasu nie mam : D punkt M (x√2,0) punkt D (0,2x)

	0−2x		−2
prosta MD −> a=		=		= −√2
	x√2−0		√2

punkt A(0,0) punkt C(2√2x,2x}

	2x−0		√2
prosta AC −> a1 =		=
	2√2x−0		2

korzystajac ze wzoru na kat miedzy prostymi

	√2   | + √2|   2		3√2   2
tg δ =		=
	√2   |1+( * (−√2))|   2		|1−1|

skoro wyszlo nam dzielenie przez zero, a jest to tangens, to musi to byc kat dla ktorego tangens nie istnieje zatem kat miedzy prostymi to 90stopni... no chyba ze cos skopalem i wgl, to trudno, nie mam czasu : D

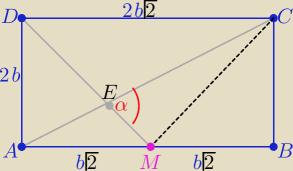Eta: Jeden ze sposobów] : z widocznym trapezem |AC|= √4b²+8b²= 2b√3 , |DM|=√4b²+2b²=b √6 P(trapezuAMCD)= (3b√2)*b= 3b²√2

	1
i P(AMCD)=		|AC|*|DM|*sinα = ...... =3b2√2*sinα
	2

porównując pola otrzymujemy ... sinα=1 ⇒ α=90^o