Wyznacz równanie symetralnej stokrotkę: Wyznacz równanie symetralnej odcinka o końcach P = (−4;3) O = (−2;5). Nie wiem czy dobrze liczę, b wychodzi mi 7, a 1.

Jerzy: Jakie masz wsp. środka PO ?

stokrotkę: (−3, 4)

Jack:

	5−3		2
a =		=		= 1
	−2+4		2

prostopadla do niej a₁ = − 1 symetralna czyli prostopadla przechodzaca przez srodek... srodek odcinka S(−3,4) zatem y = −1(x+3)+4 = −x+1

stokrotkę: Ostatnia linia to jest ze wzoru kanonicznego? Nie do końca rozumiem tę końcówkę właśnie.

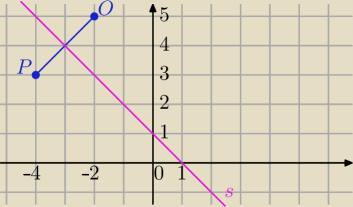
Mila: P = (−4;3) ,O = (−2;5) Każdy punkt symetralnej odcinka jest jednakowo odległy od końców tego odcinka. Niech P=(x,y) należy do symetralnej PO⇔ √(x+4)²+(y−3)²=√(x+2)²+(y−5)² /²⇔ x²+8x+16+y²−6y+9= x²+4x+4+y²−10y+25 8x+16−6y+9= 4x+4−10y+25⇔ 8x−4x−4=−4y 4x−4=−4y s: y=−x+1

jc: Nie rozumiem, może to jakieś szkolne skróty, ale nie wiedziałbym jak to ocenić (sam wynik ok). O−P = (2,2), S = (1/2)(O+P)=(−3,4) Symetralna = prosta prostopadła do O−P przechodząca przez S: 2(x+3) + 2(y−4) = 0, czyli x+y = 1

jc: Moja uwaga odnosiła się do wpisu z 16:17. 16:39 Oczywiście, że tak, ale po co tyle liczyć. Jest to jednak dobry sposób na znalezienie punktów równoodległych od A, B, C w R³.

Mila: Jack rozwiązał tak, jak uczą w szkole. jc Twojego sposobu raczej maturzyści nie zrozumieją.

Jack: dokladnie, jc nie rozumiem

jc: Nie ma już w szkole iloczynu skalarnego?

Jack: moze cos na fizyce wspomniane...ale tak to nie

jc: Jack, czym jest a i a₁? Zapewne to jakiś skrót.

Jack: "a" nazwalem jako wspolczynnik kierunkowy prostej przechodzacej przez punkty P i O "a₁" to wspolczynnik prostej prostopadlej do prostej P i O

jc: Odnośnie iloczynu skalarnego. Szkoda, że nie ma, bo potem studenci mają problemy.

jc: Dziękuję, rozumiem

6latek : Bo jak nie policza a i b to nie zrobia tego zadania inaczej Musza mieć postac kierunkowa . Jeśli by była ogolna to i tak by zamieniali na kierunkowa

Jack: niektorzy licza ukladem rownan...ale to jest kompletnie na okolo wg mnie...

6latek : Podejrzewam tez ze sposób Mili Pozdrawiam tez jest niezrozumialy dla wielu z nich

6latek : I co najgorszse Jack Jakub także tak pokazuje

jc: Mnie się sposób Mili podoba. Dowiadujemy się, że zbiór punktów na płaszczyźnie, równoodalonych od od 2 danych punktów, jest prostą.

6latek : definicja symetralnej mowi to samo

zef: Zasada jest taka: Masz przy sobie kartę wzorów liczysz ze wzorów, nie masz to z układu

jc: Niezupełnie: mamy dwie równoważne definiecje, ale równoważność wypadałoby uzasadnić. 6latek Mamy dane 2 punkty, np. A=(0,0), B=(3,0). Jak wygląda zbiór punktów, których odległość od A jest dwa razy większa niż odległość od B?