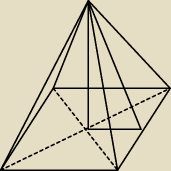
 W ostrosłupie prawidłowym czworokątnym ABCDS krawędź boczna ma długość 6, a kąt nachylenia
ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę 30 stopni. Oblicz objętość tego
ostrosłupa.
W ostrosłupie prawidłowym czworokątnym ABCDS krawędź boczna ma długość 6, a kąt nachylenia
ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę 30 stopni. Oblicz objętość tego
ostrosłupa.
| 18144√7 | ||
Wyszło mi | . Jaka jest dobra odp? | |
| 1008 |
| H | |
= tg30 | |
| a/2 |
| H | |
= sin30 | |
| h |
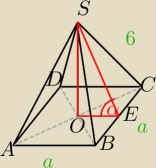
 Ściana boczna jest trójkątem równoramiennym, źle oznaczyłem na rysunku.
Ściana boczna jest trójkątem równoramiennym, źle oznaczyłem na rysunku.
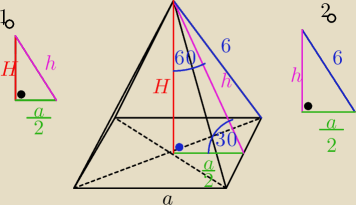 z trojkata 30,60,90.
jesli krawedz podstawy oznaczymy a, to
z trojkata 30,60,90.
jesli krawedz podstawy oznaczymy a, to
| a√3 | ||
H = | ||
| 6 |
| a√3 | ||
h = | ||
| 3 |
| a | a√3 | a | a2 | a2 | 7a2 | |||||||
62 = h2 + ( | )2 = ( | )2 + ( | )2 = | + | = | |||||||
| 2 | 3 | 2 | 3 | 4 | 12 |
| 432 | ||
a2 = | ||
| 7 |
| 12√3 | 12√21 | |||
a = | = | |||
| √7 | 7 |
| a2 | a2 | a2 | a2 | |||||
H 2 = h2 − | = | − | = | |||||
| 4 | 3 | 4 | 12 |
| a | a | a√3 | ||||
H = | = | = | ||||
| √12 | 2√3 | 6 |
| 1 | 1 | 432 | 12√21 | |||||
V = | * a2 * H = | * | * | |||||
| 3 | 3 | 7 | 7 |
| 144 * 12√21 | 1728√21 | |||
V = | = | |||
| 7*7 | 49 |
 Wprowadzam "przyjazne" oznaczenia
6a−−− dł. krawędzi podstawy to Pp=36a2
z trójkąta "ekierki" o kątach 30o,60o,90o
H=a√3 , hb=2a√3
Wprowadzam "przyjazne" oznaczenia
6a−−− dł. krawędzi podstawy to Pp=36a2
z trójkąta "ekierki" o kątach 30o,60o,90o
H=a√3 , hb=2a√3
| 12 | 2√3*√7 | |||
w trójkącie ECS : 12a2+9a2=36 ⇒ a2= | to a= | |||
| 7 | 7 |
| 6*√7 | 36*12 | |||
w trójkącie EOS : H=a√3= | i Pp=36a2= | |||
| 7 | 7 |
| 1 | 36*12 | 6√7 | ||||
V= | * | * | =................. | |||
| 3 | 7 | 7 |
| 864√7 | ||
wyszło | ||
| 49 |
| 144*6√7 | 864√7 | |||
V= | = | [j3] | ||
| 49 | 49 |