Przedziały monotoniczności funkcji Hohlik: Nie wiem do końca jak to zrobić i czy dobrze myślę..

	8x
Wyznacz przedziały monotoniczności funkcji f(x)=		. Ma maleć w (−∞;−2>,<2;∞), a
	x2+4

rosnąć w <−2;2>. x²≠−4 ⇒to zawsze prawdziwe, więc dziedzina należy do rzeczywistych. Przecięcia się z osiami: (0,0)

	8(x2+4)−8x*2x		8x2+32−16x
Tworzę pochodną: f'(x)=		=
	(x2+4)2		(x2+4)2

przyrównuję do zera, aby zbadać jak się zachowuje: 8x²−16x+32=0/:8 ⇒ x²−2x+4=0 Δ=4−16=−12 i tutaj problem, bo nie wiem co dalej robić i czy wgl dobrze to rozumiem.

Jack: nie wiem czy sformulowanie dziedzina nalezy do rzeczywistych jest poprawne...poniewaz dziedzina zawsze nalezy do rzeczywistych... raczej powinno byc D = ℛ lub D : x ∊ R a poza tym, popraw pochodna

Jack: 8x * 2x ≠ 16x

Jack: a poza tym, przedzialy monotonicznosci... widze tutaj chodzi o maxymalne... to nie musisz zadnych miejsc przeciec z osiami ani nic wystarczy f ' (x) ≥ 0 (funkcja rosnie) f ' (x) ≤ 0 (funkcja maleje) a przyrownujesz do zera zeby uzyskac ekstremum lokalne (min/max)

Hohlik: No rzeczywiście trochę dziwnie to napisałem..ale zrobiłem gafę z tym mnożeniem. Już poprawiam:

	8x2+32−16x2		−8x2+32
f'(x)=		=
	(x2+4)2		(x2+4)2

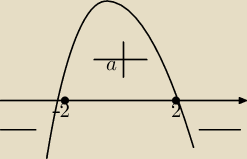
−8x²+32=0/:(−8) x²=4 x=2 ∨ x=−2 Parabola skierowana w dół, bo na początku współczynnik przy najwyższej potędze był ujemny. f↘(−∞,−2>,<2,+∞) f↗<−2,2> Dzięki Jack