geometria analityczna piotr: Witam Proszę o pomoc w takim zadaniu. Okrąg 1 o równaniu (x+6)²+(y+7)²=50 oraz okrąg 2 o środku S(−3,−10) są wewnętrznie styczne, przy czym okrąg 2 zawiera się w kole opisanym nierównością (x+6)²+(y+7)²<=50 Napisz równanie wspólnej stycznej do obu okręgów. Mam dwa środki wiec mogę obliczyć drugi promień i skoro są styczne wewnętrznie to |S1S1|=|r1−r2| i korzystając z tego równania wychodzą mi dwa promienie r2=2√2 lub r2=8√2. Mógłby mi ktoś wyjaśnić czemu wychoądza dwa promienie i jak wybrać dobry.

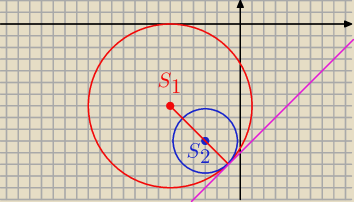
Janek191: S₁ = ( − 6, − 7) S₂ = ( −3, −10) Prosta S₁S₂

	− 10 + 7
a =		= − 1
	− 3 + 6

więc prosta styczna ma równanie y = x + b ⇒ x − y + b = 0 Jej odległość od S₁ jest równa r₁ = 5√2 zatem

I 1*(−6) − 1*(−7) + b I
	= 5√2 / *√2
√2

I b + 1 I = 10 b = − 11 lub b = 9 Odp. y = x − 11 ===========

piotr: tym spsobem też robiłem dziekuje i zatrzymuje sie na tym kiedy wychądzą mi dwa b skąd mam wiedzieć któe jest poprawne?

6latek : masz to wiedzieć ze szkoły podstawowej y=ax+b takie jest równanie prostej wspolczynnik b w tym rownaniau informuje nas w jakim punkcie wykres przetnie os Oy Jeśli zrobiles rysunek do zadania to widzisz ze b w tym zadaniu nie może być rowne 9 bo prosta y=x+9 nie będzie styczna do obu okregow (ale to należy sobie narysować

Janek191: Można wyznaczyć punkt styczności tych okręgów.

piotr: wiem o czym informuje współczynnik b tylko na maturze nie ma pkt za zczytanie informacji z rysunku pomocniczego wszystko musi być poparte odpowiednimi obliczeniami

piotr: dzieki wielkie za pomoc, mogłby jeszcze tylko ktoś wyjaśnić mi czemu jeśli podstawiam to tego równania jak napsiałem w temacie wychoądzą mi dwa możliwe promienie dla r2...

6latek : Czy jeśli na maturze dostaniesz takie zadaniae Wyznacz liczbe rozwiazan (piszse z glowy równania ||x+3|−4|=k w zaleznosci od k to będziesz to robil graficznie czy algebraicznie ja bym robil graficznie

Janek191: S₂ = ( −3, − 10) I S₁S₂ I = 3√2 r₂ = r₁ − 3√2 = 5√2 − 3√2 = 2√2 więc

I 1*(−3) − 1*(−10) + b I
	= 2√2 / * √2
√2

I b + 7 I = 4 b = − 11 lub b = − 3 Biorę b = − 11 ============

piotr: no algebraicznie nawet nie wiedziałbym jak to zrobić wiem o co chodzi z tym b niby prosty przykład ale nie mam pomysłu zeby to algebraicznie sprawdzić

piotr: znam taki wzór jeśli okręgi są styczne wewnętrznie : |S1S2|= |r1−r2| i ta wartość bezwzględna jest tylko po to jakby promienie były nieznane jeśli wiem który promień jest większy to moge tą wartość bezwzgl. mominąć tak ? dobrze myśle ?

6latek : Pewnie należy to rozumowc tak |s₁s₂| to zapis odleglosci miedzy srodkami tych okregow natomiast natomiast r₁−r−2 jest wzięte w wartość bezwzgledna dlatego ze gdyby się okazało ze r₁−r₂ <0 a odleglosc nie może być liczba ujemna to wtedy wartos cbezwzgledna z liczy ujemnej jest liczba dodatnia . Chyba o to chodzi

6latek : Ale to musi się ktoś jeszcze wypowiedzieć na ten temat

6latek : Nie podziekowale Ecie za rozwiązanie zadań (wiesz których